题目内容

14．已知圆O的半径为定长r，点A是平面内一定点（不与O重合），P是圆O上任意一点，线段AP的垂直平分线l和直线OP相交于点Q，当点P在圆上运动时，点Q的轨迹可能是下列几种：①椭圆，②双曲线，③抛物线，④直线，⑤点（　　）
A．①②⑤B．①②③C．①④⑤D．②③④

分析 对A的位置进行讨论，利用中垂线的性质即可得出QO和QP的关系，根据圆锥曲线的定义得出结论．

解答 解：∵线段AP的垂直平分线l和直线OP相交于点Q，
∴QA=QP，
（1）若A在圆外，则|QO-OP|=OP，即|QO-QA|=r＜OA，
此时Q点轨迹为双曲线；
（2）若A在圆内，则|QA+QO|=|QP+QO|=r＞OA，
此时Q点轨迹为椭圆；
（3）若A在圆上，则AP的中垂线经过圆心O，过Q点轨迹为圆心O，
故选A．

点评 本题考查了圆锥曲线的定义，属于中档题．

练习册系列答案
相关题目
4．已知△ABC中，若sin2A+sin2B＜sin2C，则这个三角形一定是（　　）
A．锐角三角形B．钝角三角形C．直角三角形D．等腰三角形
5．某次数学考试试题中共有10道选择题，每道选择题都有4个选项，其中仅有一个是正确的．评分标准规定：“每题只选1项，答对得5分，不答或答错得0分．”某考生每道题都给了一个答案，已确定有6道题的答案是正确的，而其余题中，有两道题都可判断出两个选项是错误的有一道题可以判断一个选项是错误的，还有一道题因不理解题意只能乱猜，试求出该考生：
（Ⅰ）得45分的概率；
（Ⅱ）所得分数ξ的数学期望．
2．满足A=60°，a=2$\sqrt{3}$，b=4的△ABC的个数是（　　）
A．0B．1C．2D．3
9．2011年，国际数学协会正式宣布，将每年的3月14日设为国际数学节，来源则是中国古代数学家祖冲之的圆周率．祖冲之，在世界数学史上第一次将圆周率（π）值计算到小数点后的第7位，即3.1415926到3.1415927之间，数列{an}是公差大于0的等差数列，其前三项是“31415926”中连续的三个数，数列{bn}是等比数列，其公比大于1的正整数且前三项是“31415926”中的三个数，且a3=b3．
（Ⅰ）求数列{an}，{bn}的通项公式；
（Ⅱ）cn=$\left\{\begin{array}{l}{\frac{32}{（{a}_{n}+3）•（{a}_{n+2}+3）}，n=2k-1（k∈N*）}\\{lo{g}_{3}{b}_{n+1}，n=2k（k∈N*）}\end{array}\right.$，求c1+c2+c3+…+c${\;}_{{2}^{n}}$．（n∈N*）
19．在△ABC中，内角A，B，C的对边分别为a，b，c，向量$m=（\frac{1}{2}cosA，\frac{1}{2}cosC）$，n=（c，a），且m∥n，则△ABC为等腰或直角三角形．
6．已知实数x，y满足$\left\{\begin{array}{l}3x-2y-3≤0\\ x-3y+6≥0\\ 2x+y-2≥0\end{array}\right.$，在这两个实数x，y之间插入三个实数，使这五个数构成等差数列，那么这个等差数列最后三项和的最大值为（　　）
A．11B．10C．9D．8
3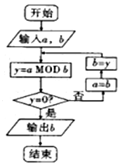．如图的程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”，执行该程序框图（图中“aMODb”表示a除以b的余数），若输入的a，b分别为485，270，则输出的b=（　　）
A．0B．10C．5D．55
4．已知函数$f（x）=sin\frac{πx}{6}$，集合M={0，1，2，3，4，5，6，7，8}，现从M中任取两个不同元素m，n，则f（m）f（n）=0的概率为（　　）
A．$\frac{5}{12}$B．$\frac{7}{12}$C．$\frac{7}{18}$D．$\frac{7}{9}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网