题目内容
11.已知函数f(x)=a(lnx-2x2)-3x,a∈R.(Ⅰ)讨论函数f(x)的单调性;
(Ⅱ)当a=-1时,函数g(x)=tx2-4x+1满足对任意的x1∈(0,e],都存在x2∈[0,1],使得f(x1)≥g(x2)成立,求实数t的取值范围.
分析 (Ⅰ)求出函数的导数,通过讨论a的范围,求出函数的单调区间即可;
(Ⅱ)问题等价于f(x1)min≥g(x2)min,根据函数的单调性分别求出函数的最小值,求出t的范围即可.
解答 解:(Ⅰ)函数f(x)的定义域是(0,+∞),
f′(x)=$\frac{a}{x}$-4ax-3=$\frac{-4{ax}^{2}-3x+a}{x}$,
a=0时,f′(x)<0,则函数f(x)在(0,+∞)递减;
a≠0时,令f′(x)=0,得方程-4ax2-3x+a=0(*),△=9+16a2>0,
方程(*)的两根分别是x1=$\frac{3+\sqrt{9+1{6a}^{2}}}{-8a}$,x2=$\frac{3-\sqrt{9+1{6a}^{2}}}{-8a}$,
a>0时,x1<0<x2,可知x∈(0,x2)时,f′(x)>0,x∈(x2,+∞)时,f′(x)<0,
即函数f(x)在(0,x2)递增,在(x2,+∞)递减;
a<0时,x2<0<x1,可知x∈(0,x1)时,f′(x)<0,x∈(x1,+∞)时,f′(x)>0,
即函数f(x)在(0,x1)递减,在(x1,+∞)递增;
综上:a=0时,函数f(x)在(0,+∞)递减;
a>0时,函数f(x)在(0,x2)递增,在(x2,+∞)递减;
a<0时,函数f(x)在(0,x1)递减,在(x1,+∞)递增;
(Ⅱ)a=-1时,f(x)=-lnx+2x2-3x,
对任意x1∈(0,e],都存在x2∈[0,1],使得f(x1)≥g(x2)成立,等价于f(x1)min≥g(x2)min,
∵f′(x)=-$\frac{1}{x}$+4x-3=$\frac{(4x+1)(x-1)}{x}$,
令f′(x)=0,解得:x=1或x=-$\frac{1}{4}$(舍),
x∈(0,1)时,f′(x)<0,函数f(x)递减,x∈(1,e]时,f′(x)>0,函数f(x)递增,
∴x∈(0,e]时,f(x)min=f(1)=-1;
而g(x)=t${(x-\frac{2}{t})}^{2}$+1-$\frac{4}{t}$,x∈[0,1],
$\frac{2}{t}$<0即t<0时,g(x)在[0,1]递减,
故g(x)min=g(1)=t-3,
由$\left\{\begin{array}{l}{t<0}\\{t-3≤-1}\end{array}\right.$,得t<0,
0<$\frac{2}{t}$<1即t>2时,g(x)min=g($\frac{2}{t}$)=1-$\frac{4}{t}$,
由$\left\{\begin{array}{l}{t>2}\\{0<t≤2}\end{array}\right.$,得t不存在,
$\frac{2}{t}$≥1即0<t≤2时,g(x)在[0,1]递减,
故g(x)min=g(1)=t-3,由$\left\{\begin{array}{l}{0<t≤2}\\{t-3≤-1}\end{array}\right.$,得0<t≤2,
故t=0时,g(x)=-4x+1,g(x)在[0,1]递减,g(x)min=g(1)=-3<-1成立,
综上,t的范围是(-∞,2].
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,转化思想,是一道综合题.

| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
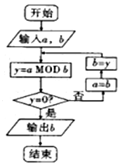 如图的程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”,执行该程序框图(图中“aMODb”表示a除以b的余数),若输入的a,b分别为485,270,则输出的b=( )
如图的程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”,执行该程序框图(图中“aMODb”表示a除以b的余数),若输入的a,b分别为485,270,则输出的b=( )