题目内容
10.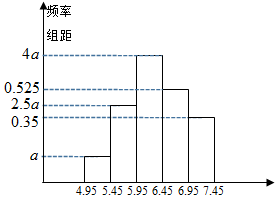 质检部门抽查某批次产品的质量(单位:克),随机检查了其中80件产品,根据样本数据描绘的频率分布直方图如下:
质检部门抽查某批次产品的质量(单位:克),随机检查了其中80件产品,根据样本数据描绘的频率分布直方图如下:(1)求频率分布直方图中a的值;
(2)若质量在[5.95,6.95)中的产品才算一级品,求在抽查的样本中一级产品共有多少件?
分析 (1)由频率分布直方图中小矩形的面积之和为1,能求出a.
(2)由频率分布直方图求出质量在[5.95,6.95)中的产品所占频率,由此能求出在抽查的样本中一级产品共有多少件.
解答 解:(1)由频率分布直方图,知:
(a+2.5a+4a+0.525+0.35)×0.5=1,
解得a=0.15.
(2)质量在[5.95,6.95)中的产品才算一级品,
由频率分布直方图得质量在[5.95,6.95)中的产品所占频率为(4×0.15+0.525)×0.5=0.5625,
∴在抽查的样本中一级产品共有:0.5625×80=45件.
点评 本题考查频率分布直方图等基础知识,考查数据处理能力、运算求解能力,考查化归与转化思想、数形结合思想,是基础题.

练习册系列答案
相关题目
18.已知$sin2α=\frac{3}{4}$,则$tanα+\frac{1}{tanα}$=( )
| A. | $\frac{8}{3}$ | B. | $\frac{10}{3}$ | C. | $\frac{11}{3}$ | D. | 4 |
15.若圆x2+y2-3x-4y-5=0关于直线ax-by=0(a>0,b>0)对称,则双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的离心率为( )
| A. | $\frac{4}{3}$ | B. | $\frac{5}{3}$ | C. | $\frac{5}{4}$ | D. | $\frac{7}{4}$ |
2.满足A=60°,a=2$\sqrt{3}$,b=4的△ABC的个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
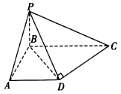 如图,在四棱锥P-ABCD中,已知PB⊥底面ABCD,BC⊥AB,AD∥BC,AB=AD=2,CD⊥PD,异面直线PA与CD所成角等于60°.
如图,在四棱锥P-ABCD中,已知PB⊥底面ABCD,BC⊥AB,AD∥BC,AB=AD=2,CD⊥PD,异面直线PA与CD所成角等于60°.