题目内容
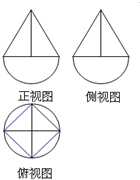 某几何体的三视图如图所示,其中正视图由直径为2的半圆和等边三角形构成,则该几何体的体积为( )
某几何体的三视图如图所示,其中正视图由直径为2的半圆和等边三角形构成,则该几何体的体积为( )A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
考点:由三视图求面积、体积
专题:计算题,空间位置关系与距离
分析:几何体是半球与正四棱锥的组合体,根据三视图判断半球的直径及四棱锥的侧棱长,底面正方形的对角线长,求得底面正方形的边长及棱锥的高,
把数据代入半球与棱锥的体积公式计算.
把数据代入半球与棱锥的体积公式计算.
解答:
解:由三视图知:几何体是半球与正四棱锥的组合体,
其中半球的直径为2,四棱锥的侧棱长为2,底面正方形的对角线长为2,
∴底面正方形的边长为
.棱锥的高为
=
∴几何体的体积V=
π×13+
×(
)2×
=
+
.
故选:C.
其中半球的直径为2,四棱锥的侧棱长为2,底面正方形的对角线长为2,
∴底面正方形的边长为
| 2 |
| 4-1 |
| 3 |
∴几何体的体积V=
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 2π |
| 3 |
2
| ||
| 3 |
故选:C.
点评:本题考查了由三视图求几何体的体积,根据三视图判断几何体的形状及相关几何量的数据是解题的关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
执行如图所示的程序框图,则输出的结果为( )


| A、2 | ||
| B、1 | ||
C、
| ||
| D、-1 |
复数
为纯虚数,则实数a的值为( )
| 3-ai |
| 2+3i |
| A、1 | B、-1 | C、2 | D、-2 |
Rt△ABC中CA=CB=
,M为AB的中点,将△ABC沿CM折叠,使A、B之间的距离为1,则三棱锥M-ABC外接球的表面积为( )
| 2 |
A、
| ||
| B、4π | ||
| C、3π | ||
D、
|
某旅馆有三人间、两人间、单人间三种房间各一间,有3位成人带2个小孩来住宿,小孩必须有成人陪同,则不同的住宿方法有( )
| A、18种 | B、21种 |
| C、27种 | D、35种 |
已知i为虚数单位,复数z=-
+
i的共轭复数为
,则
+|z|( )
| 1 |
| 2 |
| ||
| 2 |
. |
| z |
. |
| z |
A、-
| ||||||
B、
| ||||||
C、
| ||||||
D、-
|