题目内容
| 2sin40°-cos10° |
| sin10° |
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
考点:两角和与差的正弦函数
专题:三角函数的求值
分析:先把sin40°转换为sin(10°+30°),进而利用两角和与差的正弦函数展开,化简整理即可.
解答:
解:
=
=
=
=
,
故选B
| 2sin40°-cos10° |
| sin10° |
| 2sin(10°+30°)-cos10° |
| sin10° |
2(
| ||||||
| sin10° |
| ||
| sin10° |
| 3 |
故选B
点评:本题主要考查了两角和与差的正弦函数.解题的关键是把sin40°转换为sin(10°+30°).

练习册系列答案
相关题目
复数
为纯虚数,则实数a的值为( )
| 3-ai |
| 2+3i |
| A、1 | B、-1 | C、2 | D、-2 |
已知i为虚数单位,复数z=-
+
i的共轭复数为
,则
+|z|( )
| 1 |
| 2 |
| ||
| 2 |
. |
| z |
. |
| z |
A、-
| ||||||
B、
| ||||||
C、
| ||||||
D、-
|
在△ABC中,∠A<30°是cosA>
的( )
| 1 |
| 2 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
若存在正实数M,对于任意x∈(1,+∞),都有|f(x)|≤M,则称函数f(x)在(1,+∞) 上是有界函数.下列函数:
①f(x)=
;
②f(x)=
;
③f(x)=
;
④f(x)=xsinx.
其中“在(1,+∞)上是有界函数”的序号为( )
①f(x)=
| 1 |
| x-1 |
②f(x)=
| x |
| x2+1 |
③f(x)=
| lnx |
| x |
④f(x)=xsinx.
其中“在(1,+∞)上是有界函数”的序号为( )
| A、②③ | B、①②③ |
| C、②③④ | D、③④ |
一个空间几何体的三视图如图所示,则该几何体的体积为( )
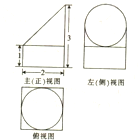

A、4+
| ||
| B、4+π | ||
| C、4+2π | ||
| D、以上都不对 |