题目内容
一动圆截直线3x-y=0和直线3x+y=0所得弦长分别为8，6，求动圆圆心的轨迹方程．
考点：轨迹方程
专题：综合题,直线与圆
分析：设动圆圆心为M，由动圆截两直线所得的弦长，结合点到直线的距离公式，根据半径相等列关于动圆圆心坐标的关系式，整理后得答案．
解答：
解：如图，
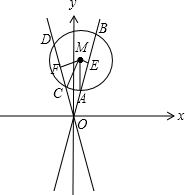
设动圆圆心M点的坐标为（x，y），⊙M分别截直线3x-y=0和3x+y=0所得弦分别为AB，CD，
则|AB|=8，|CD|=6，过M分别作直线3x-y=0和3x+y=0的垂线，垂足分别为E，F，则|AE|=4，|CF|=3，
由点到直线的距离公式得|ME|=
，|MF|=
，
∵|AE|2+|ME|2=|CF|2+|MF|2，
∴16+
=9+
，整理得：xy=
．
∴动圆圆心M的轨迹方程是：xy=
．
设动圆圆心M点的坐标为（x，y），⊙M分别截直线3x-y=0和3x+y=0所得弦分别为AB，CD，
则|AB|=8，|CD|=6，过M分别作直线3x-y=0和3x+y=0的垂线，垂足分别为E，F，则|AE|=4，|CF|=3，
由点到直线的距离公式得|ME|=
| |3x-y| | ||
|
| |3x+y| | ||
|
∵|AE|2+|ME|2=|CF|2+|MF|2，
∴16+
| (3x-y)2 |
| 10 |
| (3x+y)2 |
| 10 |
| 35 |
| 6 |
∴动圆圆心M的轨迹方程是：xy=
| 35 |
| 6 |
点评：本题考查了轨迹方程，考查了点到直线的距离公式，训练了数形结合的解题思想方法，解答的关键是由东圆的半径相等列出函数关系式，是中档题．
练习册系列答案
相关题目
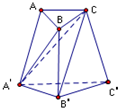如图所示，三棱台ABC-A′B′C′中，AB：A′B′=1：2，则三棱锥C-A′B′C′，B-A′B′C，A′-ABC的体积之比为（ ）| A、1：1：1 |
| B、2：1：1 |
| C、4：2：1 |
| D、4：4：1 |
已知曲线C：x2+y2-2x+2y=0与直线L：y+2=k（x-2），则C与L的公共点（ ）
| A、有2个 | B、最多1个 |
| C、至少1个 | D、不存在 |
圆柱的一个底面积为S，侧面展开图是一个正方形，那么这个圆柱的体积是（ ）
A、
| ||||
B、
| ||||
C、2S
| ||||
D、S
|
在区域D：（x-1）2+y2≤4内随机取一个点，则此点到点A（1，2）的距离大于2的概率是（ ）
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
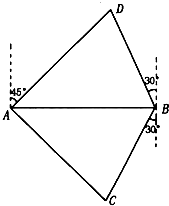如图，A，B是海面上位于东西方向相距