题目内容
在满足不等式组
的平面点集中随机取一点M(x0,y0),设事件A=“y0<2x0”,那么事件A发生的概率是( )
|
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:概率与统计
分析:确定不等式组表示的区域,求出面积,求出满足y<2x的区域的面积,利用几何概型概率公式,可得结论.
解答:
 解:作出不等式组
解:作出不等式组
的平面区域即△ABC,其面积为4,
且事件A=“y0<2x0”表示的区域为△AOC,其面积为3,
∴事件A发生的概率是
.
故选B.
 解:作出不等式组
解:作出不等式组
|
且事件A=“y0<2x0”表示的区域为△AOC,其面积为3,
∴事件A发生的概率是
| 3 |
| 4 |
故选B.
点评:本题考查几何概型,考查不等式组表示的平面区域,确定以面积为测度,正确计算面积是关键,属于中档题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
在区域D:(x-1)2+y2≤4内随机取一个点,则此点到点A(1,2)的距离大于2的概率是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
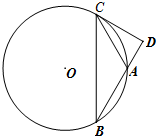 【几何证明选讲选做题】
【几何证明选讲选做题】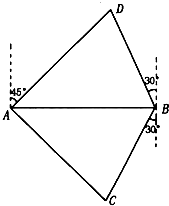 如图,A,B是海面上位于东西方向相距
如图,A,B是海面上位于东西方向相距 如图是一块带有圆形空洞和方形空洞的小木板,则下列物体中既可以堵住圆形空洞,又可以堵住方形空洞的是( )
如图是一块带有圆形空洞和方形空洞的小木板,则下列物体中既可以堵住圆形空洞,又可以堵住方形空洞的是( )


