题目内容
在面积为1的正方形ABCD内部随机取一点P,则△PAB的面积大于等于
的概率是( )
| 1 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:概率与统计
分析:设E、F分别为AD、BC的中点,可得四边形ABFE是矩形.当点P落在线段EF上时,△PAB的面积等于矩形ABFE面积的一半,可得此时S△ABP=
S矩形ABFE=
,由此可得当点P落在矩形CDEF内部或在EF上时△PAB的面积大于等于
.
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
解答:
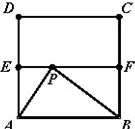 解:设正方形ABCD中,E、F分别为AD、BC的中点
解:设正方形ABCD中,E、F分别为AD、BC的中点
∵四边形ABCD是正方形,E、F分别为AD、BC的中点
∴EF∥AB且EF=AB,可得四边形ABFE是矩形
∵正方形ABCD面积为1,∴AB=1且AE=
AD=
.
当点P落在线段EF上时,△PAB的面积等于矩形ABFE面积的一半,
此时S△ABP=
S矩形ABFE=
,
因此,当点P落在正方形ABCD内部,且在线段EF上或EF的上方时,
可使△PAB的面积大于等于
,
∴△PAB的面积大于等于
的概率为P=
=
.
故选B.
 解:设正方形ABCD中,E、F分别为AD、BC的中点
解:设正方形ABCD中,E、F分别为AD、BC的中点∵四边形ABCD是正方形,E、F分别为AD、BC的中点
∴EF∥AB且EF=AB,可得四边形ABFE是矩形
∵正方形ABCD面积为1,∴AB=1且AE=
| 1 |
| 2 |
| 1 |
| 2 |
当点P落在线段EF上时,△PAB的面积等于矩形ABFE面积的一半,
此时S△ABP=
| 1 |
| 2 |
| 1 |
| 4 |
因此,当点P落在正方形ABCD内部,且在线段EF上或EF的上方时,
可使△PAB的面积大于等于
| 1 |
| 4 |
∴△PAB的面积大于等于
| 1 |
| 4 |
| SCDEF |
| SABCD |
| 1 |
| 2 |
故选B.
点评:本题考查几何概型,着重考查了正方形的性质、三角形面积公式和几何概型计算公式等知识,属于基础题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
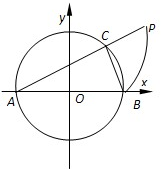 如图,在直角坐标系xoy中,AB是半圆O:x2+y2=1(y≥0)的直径,点C是半圆O上任一点,延长AC到点P,使CP=CB,当点C从点B运动到点A时,动点P的轨迹的长度是( )
如图,在直角坐标系xoy中,AB是半圆O:x2+y2=1(y≥0)的直径,点C是半圆O上任一点,延长AC到点P,使CP=CB,当点C从点B运动到点A时,动点P的轨迹的长度是( )| A、2π | ||
B、
| ||
| C、π | ||
D、4
|
经过两点A(4,2y+1),B(2,-3)的直线的倾斜角为
,则y=( )
| 3π |
| 4 |
| A、-1 | B、0 | C、-3 | D、2 |
曲线y=x-
在点(1,0)处的切线方程为( )
| 1 |
| x |
| A、y=2x-2 |
| B、y=x-1 |
| C、y=0 |
| D、y=-x+1 |
 如图,点A、B、C、D在⊙O上,O点在∠D的内部,四边形OABC为平行四边形,则∠OAD+∠OCD=
如图,点A、B、C、D在⊙O上,O点在∠D的内部,四边形OABC为平行四边形,则∠OAD+∠OCD= 在边长为10的正方形ABCD内有一动点P,AP=9,作PQ⊥BC于Q,PR⊥CD于R,求矩形PQCR面积的最小值和最大值,并指出取最大值时P的具体位置.
在边长为10的正方形ABCD内有一动点P,AP=9,作PQ⊥BC于Q,PR⊥CD于R,求矩形PQCR面积的最小值和最大值,并指出取最大值时P的具体位置.