题目内容
锐角△ABC中,角A,B所对的边长分别为a,b,若2asinB=b,则角A等于 .
考点:正弦定理的应用
专题:解三角形
分析:根据正弦定理,把2asinB=b化为2sinAsinB=sinB,求出sinA,即得A的值.
解答:
解:在△ABC中,由正弦定理,∵2asinB=b,
∴2sinAsinB=sinB;
又∵sinB≠0,
∴sinA=
;
又∵△ABC为锐角三角形,
∴A=
.
故答案为:
.
∴2sinAsinB=sinB;
又∵sinB≠0,
∴sinA=
| 1 |
| 2 |
又∵△ABC为锐角三角形,
∴A=
| π |
| 6 |
故答案为:
| π |
| 6 |
点评:本题考查了锐角三角形的定义、正弦定理与解三角方程的问题,意在考查学生的转化能力与三角变换能力,是基础题.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
为研究学生物理成绩与数学成绩是否相关,某高中数学老师将一次考试中的五名学生的数学成绩x、物理成绩y列表如下:
根据上表提供的数据,若求得y关于x的线性回归方程为
=0.75x+20.25,则表中t的值为( )
| 学生 | A1 | A2 | A3 | A4 | A5 |
| x(分) | 89 | 91 | 93 | 95 | 97 |
| y(分) | 87 | 89 | t | 92 | 93 |
 |
| y |
| A、88 | B、89 | C、90 | D、91 |
若直线l:y=kx-
与直线2x+3y-6=0的交点位于第一象限,则直线l的倾斜角的取值范围是( )
| 3 |
A、[
| ||||
B、[
| ||||
C、(
| ||||
D、(
|
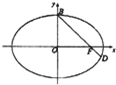 如图,已知F是椭圆C的一个焦点,B是短轴的一个端点,线段BF的延长线交椭圆C于点D,且
如图,已知F是椭圆C的一个焦点,B是短轴的一个端点,线段BF的延长线交椭圆C于点D,且