题目内容
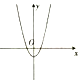
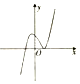
8.抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,圆M与y轴相切,过原点O作倾斜角为$\frac{π}{3}$的直线m,交直线l于点A,交圆M于不同的两点O、B,且|AO|=|BO|=2,若P为抛物线C上的动点,则$\overrightarrow{PM}•\overrightarrow{PF}$的最小值为( )| A. | -2 | B. | 2 | C. | $\frac{7}{4}$ | D. | 3 |
分析 求出p的值,从而求出抛物线方程,求出圆心和半径可求出⊙M的方程,表示出$\overrightarrow{PM}•\overrightarrow{PF}$,然后根据点在抛物线上将y消去,求关于x 的二次函数的最小值即可;
解答 解:因为$\frac{p}{2}$=OA•cos$\frac{π}{3}$=2×$\frac{1}{2}$=1,即p=2,所以抛物线C的方程为y2=4x,
设⊙M的半径为r,则$\frac{OB}{2}•\frac{1}{cos\frac{π}{3}}$=2,所以⊙M的方程为(x-2)2+y2=4
设P(x,y)(x≥0),则$\overrightarrow{PM}•\overrightarrow{PF}$=x2-3x+2+y2=x2+x+2,
所以当x=0时,有最小值为2
故选:B
点评 本题主要考查了圆的方程和抛物线方程,以及向量数量积的最值,属于中档题.

练习册系列答案
相关题目
3.设F1,F2是椭圆$\frac{x^2}{a^2}+\frac{y^2}{25}=1(a<5)$的两个焦点,且|F1F2|=8,弦AB过点F2,则△ABF1的周长为( )
| A. | 12 | B. | 20 | C. | 2$\sqrt{41}$ | D. | 4$\sqrt{41}$ |
17.为了得到函数y=4cos2x的图象,只需将函数$y=4cos(2x+\frac{π}{4})$的图象上每一个点( )
| A. | 横坐标向左平动$\frac{π}{4}$个单位长度 | B. | 横坐标向右平移$\frac{π}{4}$个单位长度 | ||
| C. | 横坐标向左平移$\frac{π}{8}$个单位长度 | D. | 横坐标向右平移$\frac{π}{8}$个单位长度 |
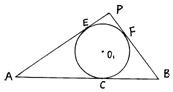 如图,△PAB的顶点A、B为定点,P为动点,其内切圆O1与AB、PA、PB分别相切于点C、E、F,且$AB=2\sqrt{3}$,||AC|-|BC||=2.
如图,△PAB的顶点A、B为定点,P为动点,其内切圆O1与AB、PA、PB分别相切于点C、E、F,且$AB=2\sqrt{3}$,||AC|-|BC||=2.