题目内容
3.设F1,F2是椭圆$\frac{x^2}{a^2}+\frac{y^2}{25}=1(a<5)$的两个焦点,且|F1F2|=8,弦AB过点F2,则△ABF1的周长为( )| A. | 12 | B. | 20 | C. | 2$\sqrt{41}$ | D. | 4$\sqrt{41}$ |
分析 由题意可知:焦点在y轴上,|F1F2|=8,即a=5,c=3,由△ABF1的周长l=|AF1|+|BF1|+|AB|=|AF1|+|BF1|+|AF2|+|BF2|=4a=20,即可求得△ABF1的周长.
解答 解:由题意可知:椭圆$\frac{x^2}{a^2}+\frac{y^2}{25}=1(a<5)$,焦点在y轴上,|F1F2|=8,即a=5,c=3,
据椭圆的定义可知:|F1A|+|AF2|=2a=10,|F1B|+|BF2|=2a=10,
由△ABF1的周长l=|AF1|+|BF1|+|AB|=|AF1|+|BF1|+|AF2|+|BF2|=4a=20,
∴△ABF1的周长20,
故选B.
点评 本题考查椭圆的定义及标准方程的应用,考查焦点三角形的周长公式,考查计算能力,属于基础题.

练习册系列答案
相关题目
14.抛物线x=4y2的焦点坐标是 ( )
| A. | ($\frac{1}{16}$,0) | B. | (1,0) | C. | (0,$\frac{1}{16}$) | D. | (0,1 ) |
11.已知命题p:?x0∈R,lnx0≥x0-1.命题q:?θ∈R,sinθ+cosθ>-1.则下列命题中为真命题的是( )
| A. | p∧(?q) | B. | (?p)∨q | C. | (?p)∧(?q) | D. | p∧q |
8.抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,圆M与y轴相切,过原点O作倾斜角为$\frac{π}{3}$的直线m,交直线l于点A,交圆M于不同的两点O、B,且|AO|=|BO|=2,若P为抛物线C上的动点,则$\overrightarrow{PM}•\overrightarrow{PF}$的最小值为( )
| A. | -2 | B. | 2 | C. | $\frac{7}{4}$ | D. | 3 |
13.已知命题p:?x∈(0,+∞),3x-cosx>0,则下列叙述正确的是( )
| A. | ¬p:?x∈(0,+∞),3x-cosx≤0 | B. | ¬p:?x∈(0,+∞),3x-cosx<0 | ||
| C. | ¬p:?x∈(-∞,0],3x-cosx≤0 | D. | ¬p是假命题 |
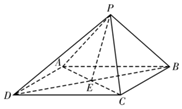 如图,四棱锥P-ABCD的底面ABCD是菱形,∠ADC=60°,PA=PC,PD⊥PB,AC∩BD=E,二面角P-AC-B的大小为60°.
如图,四棱锥P-ABCD的底面ABCD是菱形,∠ADC=60°,PA=PC,PD⊥PB,AC∩BD=E,二面角P-AC-B的大小为60°.