题目内容
17.为了得到函数y=4cos2x的图象,只需将函数$y=4cos(2x+\frac{π}{4})$的图象上每一个点( )| A. | 横坐标向左平动$\frac{π}{4}$个单位长度 | B. | 横坐标向右平移$\frac{π}{4}$个单位长度 | ||
| C. | 横坐标向左平移$\frac{π}{8}$个单位长度 | D. | 横坐标向右平移$\frac{π}{8}$个单位长度 |
分析 利用函数y=Asin(ωx+φ)的图象变换规律,得出结论.
解答 解:将函数$y=4cos(2x+\frac{π}{4})$的图象上每一个点横坐标向右平移$\frac{π}{8}$个单位长度,
可得y=4cos[2(x-$\frac{π}{8}$)+$\frac{π}{4}$]=4cos2x的图象,
故选:D.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,属于基础题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
7.已知点P为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右支上一点,F1,F2为双曲线的左、右焦点,使($\overrightarrow{OP}$+$\overrightarrow{O{F}_{2}}$)($\overrightarrow{OP}$-$\overrightarrow{O{F}_{2}}$)=0(O为坐标原点),且|$\overrightarrow{P{F}_{1}}$|=$\sqrt{3}$|$\overrightarrow{P{F}_{2}}$|,则双曲线离心率为( )
| A. | $\frac{\sqrt{3}+1}{2}$ | B. | $\sqrt{6}$+1 | C. | $\sqrt{3}$+1 | D. | $\frac{\sqrt{3}+1}{2}$ |
8.抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,圆M与y轴相切,过原点O作倾斜角为$\frac{π}{3}$的直线m,交直线l于点A,交圆M于不同的两点O、B,且|AO|=|BO|=2,若P为抛物线C上的动点,则$\overrightarrow{PM}•\overrightarrow{PF}$的最小值为( )
| A. | -2 | B. | 2 | C. | $\frac{7}{4}$ | D. | 3 |
5.已知数列{an}的通项公式an=n2-2n-8(n∈N*),则a4等于( )
| A. | 1 | B. | 2 | C. | 0 | D. | 3 |
7.设g(x)为定义在R上的奇函数,且g(x)不恒为0,若$f(x)=(\frac{1}{{{a^x}-1}}-\frac{1}{b})g(x)$(a>0且a≠1)为偶函数,则常数b=( )
| A. | -2 | B. | 2 | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
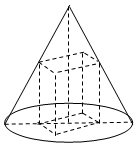 底面半径为4,高为$8\sqrt{2}$的圆锥有一个内接的正四棱柱(底面是正方形,侧棱与底面垂直的四棱柱).
底面半径为4,高为$8\sqrt{2}$的圆锥有一个内接的正四棱柱(底面是正方形,侧棱与底面垂直的四棱柱).