已知某几何体的三视图如图所示.其中俯视图中的曲线是一段半圆弧.则这个几何体的表面积是12+π．题目和参考答案——青夏教育精英家教网——

题目内容

20．已知某几何体的三视图如图所示，其中俯视图中的曲线是一段半圆弧，则这个几何体的表面积是12+π．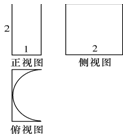

分析由已知中的三视图，可得该几何体是一个以俯视图为底面的柱体，计算各个面的面积，相加可得答案．

解答解：由已知中的三视图，可得该几何体是一个以俯视图为底面的柱体，
这是一个四棱柱挖去一个半圆柱所得几何体，
底面面积为：1×2-$\frac{1}{2}$π=2-$\frac{1}{2}$π，
底面周长为：1+2+1+π=4+π，
高为2，
故这个几何体的表面积是S=（4+π）×2+2×（2-$\frac{1}{2}$π）=12+π，
故答案为：12+π

点评本题考查的知识点是棱柱的体积表面积，半圆柱的体积和表面积，简单几何体的三视图，难度中档．

练习册系列答案

随堂练1加2系列答案

绩优学案系列答案

作业本江西教育出版社系列答案

配套练习册系列答案

课时导学案课时作业本系列答案

指南针系列答案

新课标新精编系列答案

综合素质随堂反馈系列答案

目标复习检测卷系列答案

金种子领航考卷系列答案

相关题目

10．设F₁、F₂分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右焦点，过点F₂的直线交双曲线右支于A、B两点．若AF₂⊥AF₁，且|BF₂|=2|AF₁|，则双曲线的离心率为（　　）

$\frac{\sqrt{17}}{3}$

$\frac{\sqrt{10}}{2}$

$\frac{\sqrt{58}}{4}$

11．已知命题p：?x₀∈R，lnx₀≥x₀-1．命题q：?θ∈R，sinθ+cosθ＞-1．则下列命题中为真命题的是（　　）

（?p）∧（?q）

8．抛物线C：y²=2px（p＞0）的准线为l，焦点为F，圆M的圆心在x轴的正半轴上，圆M与y轴相切，过原点O作倾斜角为$\frac{π}{3}$的直线m，交直线l于点A，交圆M于不同的两点O、B，且|AO|=|BO|=2，若P为抛物线C上的动点，则$\overrightarrow{PM}•\overrightarrow{PF}$的最小值为（　　）

15．已知函数f（x）=a（x-1）²+lnx，a∈R．
（Ⅰ）当$a=-\frac{1}{4}$时，求函数y=f（x）的单调减区间；
（Ⅱ）$a=\frac{1}{2}$时，令$h（x）=f（x）-3lnx+x-\frac{1}{2}$．求h（x）在[1，e]上的最大值和最小值；
（Ⅲ）若a≤0时，求证：函数f（x）≤x-1在x∈[1，+∞）恒成立．

5．已知数列{a_n}的通项公式a_n=n²-2n-8（n∈N^*），则a₄等于（　　）

12．已知函数f（x）=x³+3x对任意的m∈[-2，2]，f（mx-2）+f（x）＜0恒成立，则x∈（-2，$\frac{2}{3}$）．

9．已知0＜α＜$\frac{π}{2}$，cos（2π-α）-sin（π-α）=-$\frac{\sqrt{5}}{5}$
（1）求sinα+cosα的值；
（2）求$\frac{{{{cos}^2}（\frac{3π}{2}+α）+2cosαcos（\frac{π}{2}-α）}}{{1+{{sin}^2}（\frac{π}{2}-α）}}$的值．

10．已知幂函数f（x）=x${\;}^{-{m}^{2}+2m+3}$（m∈Z）为偶函数，且在区间（0，+∞）上是单调增函数．
（1）求函数f（x）的解析式；
（2）设函数g（x）=$\sqrt{f（x）}$+2x+c，若g（x）＞2对任意的x∈R恒成立，求实数c的取值范围．