题目内容
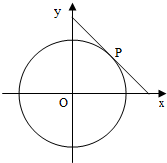 圆x2+y2=4的切线与x轴正半轴,y轴正半轴围成一个三角形,当该三角形面积最小时,切点为P(如图).
圆x2+y2=4的切线与x轴正半轴,y轴正半轴围成一个三角形,当该三角形面积最小时,切点为P(如图).(Ⅰ)求点P的坐标;
(Ⅱ)焦点在x轴上的椭圆C过点P,且与直线l:y=x+
| 3 |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)设切点P的坐标为(x0,y0),求得圆的切线方程,根据切线与x轴正半轴,y轴正半轴围成的三角形的面积S=
.再利用基本不等式求得S取得最小值,求得点P的坐标.
(Ⅱ)设椭圆的标准方程为
+
=1,a>b>0,则
+
=1.把直线方程和椭圆的方程联立方程组,转化为关于x的一元二次方程,里哦也难怪韦达定理、弦长公式求出弦长AB以及点P到直线的距离d,再由△PAB的面积为S=
•AB•d=2,求出a2、b2的值,从而得到所求椭圆的方程.
| 8 |
| x0•y0 |
(Ⅱ)设椭圆的标准方程为
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| a2 |
| 2 |
| b2 |
| 1 |
| 2 |
解答:
解:(Ⅰ)设切点P的坐标为(x0,y0),且x0>0,y0>0.
则切线的斜率为-
,故切线方程为 y-y0=-
(x-x0),即x0x+y0y=4.
此时,切线与x轴正半轴,y轴正半轴围成的三角形的面积S=
•
•
=
.
再根据 x02+y02=4≥2
,可得当且仅当x0=y0=
时,x0•y0取得最大值,即S取得最小值,
故点P的坐标为(
,
).
(Ⅱ)设椭圆的标准方程为
+
=1,a>b>0,∵椭圆C过点P,∴
+
=1.
由
求得b2x2+4
x+6-2b2=0,
∴x1+x2=-
,x1•x2=
.
由 y1=x1+
,y2=x2+
,可得AB=
|x2-x1|=
•
=
•
=
.
由于点P(
,
)到直线l:y=x+
的距离d=
,
△PAB的面积为S=
•AB•d=2,可得 b4-9b2+18=0,解得 b2=3,或 b2=6,
当b2=6 时,由
+
=1求得a2=3,不满足题意;
当b2=3时,由
+
=1求得a2=6,满足题意,故所求的椭圆的标准方程为
+
=1.
则切线的斜率为-
| x0 |
| y0 |
| x0 |
| y0 |
此时,切线与x轴正半轴,y轴正半轴围成的三角形的面积S=
| 1 |
| 2 |
| 4 |
| x0 |
| 4 |
| y0 |
| 8 |
| x0•y0 |
再根据 x02+y02=4≥2
| x0•y0 |
| 2 |
故点P的坐标为(
| 2 |
| 2 |
(Ⅱ)设椭圆的标准方程为
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| a2 |
| 2 |
| b2 |
由
|
| 3 |
∴x1+x2=-
4
| ||
| b2 |
| 6-2b2 |
| b2 |
由 y1=x1+
| 3 |
| 3 |
| 2 |
| 2 |
| (x1+x2)2-4x1•x2 |
| 2 |
(
|
=
| ||
| b2 |
| 8b4-24b2+48 |
由于点P(
| 2 |
| 2 |
| 3 |
|
| ||||||
|
△PAB的面积为S=
| 1 |
| 2 |
当b2=6 时,由
| 2 |
| a2 |
| 2 |
| b2 |
当b2=3时,由
| 2 |
| a2 |
| 2 |
| b2 |
| x2 |
| 6 |
| y2 |
| 3 |
点评:本题主要考查直线和圆相切的性质,直线和圆锥曲线的位置关系,点到直线的距离公式、弦长公式的应用,属于难题.

练习册系列答案
相关题目
已知函数f(x)=
,则f(f(2014))=( )
|
A、
| ||
B、-
| ||
| C、1 | ||
| D、-1 |
已知Rt△ABC中,AB=8,AC=4,BC=4
,则对于△ABC所在平面内的一点P,
•(
+
)的最小值是( )
| 3 |
| PA |
| PB |
| PC |
| A、-14 | B、-8 |
| C、-26 | D、-30 |
 一同学为研究函数f(x)=
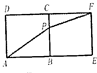
一同学为研究函数f(x)= 如图,已知二面角α-MN-β的大小为60°,菱形ABCD在面β内,A、B两点在棱MN上,∠BAD=60°,E是AB的中点,DO⊥面α,垂足为O.
如图,已知二面角α-MN-β的大小为60°,菱形ABCD在面β内,A、B两点在棱MN上,∠BAD=60°,E是AB的中点,DO⊥面α,垂足为O.
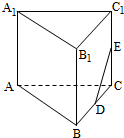 在如图所示的多面体中,四边形ABB1A1和ACC1A1都为矩形
在如图所示的多面体中,四边形ABB1A1和ACC1A1都为矩形