题目内容
已知等比数列{an}的公比大于零,a1+a2=3,a3=4,数列{bn}是等差数列,bn=
,c≠0是常数.
(1)求c的值,数列{an}与{bn}的通项公式;
(2)设数列{cn}满足:c1=1,cn-cn-1=an-1(n≥2),求数列{cn}的通项公式及使得cn-2bn≥0成立的n的取值范围.
| n(n+1) |
| n+c |
(1)求c的值,数列{an}与{bn}的通项公式;
(2)设数列{cn}满足:c1=1,cn-cn-1=an-1(n≥2),求数列{cn}的通项公式及使得cn-2bn≥0成立的n的取值范围.
考点:等比数列的性质
专题:等差数列与等比数列
分析:(1)由等差数列通项公式的特点结合bn=
可设bn=
=n+t,整理后由系数间的关系求得c=1,则等差数列{bn}的通项公式可求.再设出等比数列{an}的公比,由a1+a2=3,a3=4联立求出首项和公比,则等比数列{an}的通项公式可求;
(2)把{an}的通项公式代入cn-cn-1=an-1(n≥2),利用累加法求得数列{cn}的通项公式,再把{bn}和{cn}的通项公式代入cn-2bn≥0,通过构造辅助函数f(n)=2n-1-2n,作差判断出f(n)的单调性,结合计算f(1)<0,f(2)<0,f(3)<0,f(4)=0得答案.
| n(n+1) |
| n+c |
| n(n+1) |
| n+c |
(2)把{an}的通项公式代入cn-cn-1=an-1(n≥2),利用累加法求得数列{cn}的通项公式,再把{bn}和{cn}的通项公式代入cn-2bn≥0,通过构造辅助函数f(n)=2n-1-2n,作差判断出f(n)的单调性,结合计算f(1)<0,f(2)<0,f(3)<0,f(4)=0得答案.
解答:
解:(1)∵数列{bn}是等差数列,且bn=
,
∴bn=
=n+t,则n2+n=n2+(t+c)n+tc,
即t+c=1,且tc=0,
又c≠0,
∴t=0,则c=1.
∴bn=n.
设等比数列{an}的公比为q(q>0),
由a1+a2=3,a3=4,得:
,解得
.
∴an=2n-1;
(2)∵cn-cn-1=an-1(n≥2),
∴cn-cn-1=2n-2(n≥2),
则c2-c1=20
c3-c2=21
…
cn-cn-1=2n-2(n≥2).
累加得:cn-c1=20+21+…+2n-2=
=2n-1-1.
又c1=1,
∴cn=2n-1(n≥2).
当n=1时满足,
∴cn=2n-1.
由cn-2bn≥0,得2n-1-2n≥0,
令f(n)=2n-1-2n,
则f(n+1)-f(n)=2n-2(n+1)-2n-1+2n=2n-1-2,
当n≥2时f(n)单调递增.
又f(1)<0,f(2)<0,f(3)<0,f(4)=0.
∴n≥4.
故使得cn-2bn≥0成立的n的取值范围是[4,+∞).
| n(n+1) |
| n+c |
∴bn=
| n(n+1) |
| n+c |
即t+c=1,且tc=0,
又c≠0,
∴t=0,则c=1.
∴bn=n.
设等比数列{an}的公比为q(q>0),
由a1+a2=3,a3=4,得:
|
|
∴an=2n-1;
(2)∵cn-cn-1=an-1(n≥2),
∴cn-cn-1=2n-2(n≥2),
则c2-c1=20
c3-c2=21
…
cn-cn-1=2n-2(n≥2).
累加得:cn-c1=20+21+…+2n-2=
| 1×(1-2n-1) |
| 1-2 |
又c1=1,
∴cn=2n-1(n≥2).
当n=1时满足,
∴cn=2n-1.
由cn-2bn≥0,得2n-1-2n≥0,
令f(n)=2n-1-2n,
则f(n+1)-f(n)=2n-2(n+1)-2n-1+2n=2n-1-2,
当n≥2时f(n)单调递增.
又f(1)<0,f(2)<0,f(3)<0,f(4)=0.
∴n≥4.
故使得cn-2bn≥0成立的n的取值范围是[4,+∞).
点评:本题考查等差数列和等比数列的通项公式,训练了累加法求数列的通项公式,考查了数列的函数特性,训练了利用构造函数法求解不等式,是中高档题.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
若x,y满足约束条件
,则
的最小值为( )
|
| x |
| y |
A、
| ||
B、
| ||
| C、1 | ||
D、
|
正三棱柱ABC-A1B1C1的底面边长为2,侧棱长为
,D为BC中点,则三棱锥A-B1DC1的体积为( )
| 3 |
| A、3 | ||||
B、
| ||||
| C、1 | ||||
D、
|
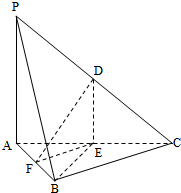 如图,在三棱锥P-ABC中,D,E,F分别为棱PC,AC,AB的中点,已知PA⊥AC,PA=6,BC=8,DF=5.求证:
如图,在三棱锥P-ABC中,D,E,F分别为棱PC,AC,AB的中点,已知PA⊥AC,PA=6,BC=8,DF=5.求证: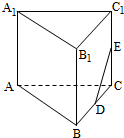 在如图所示的多面体中,四边形ABB1A1和ACC1A1都为矩形
在如图所示的多面体中,四边形ABB1A1和ACC1A1都为矩形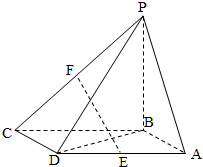 如图,四棱锥P-ABCD的底面ABCD是平行四边形,BA=BD=
如图,四棱锥P-ABCD的底面ABCD是平行四边形,BA=BD=