题目内容
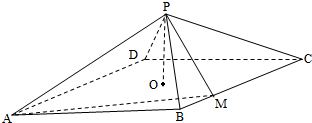 如图,四棱锥P-ABCD,底面是以O为中心的菱形,PO⊥底面ABCD,AB=2,∠BAD=
如图,四棱锥P-ABCD,底面是以O为中心的菱形,PO⊥底面ABCD,AB=2,∠BAD=| π |
| 3 |
| 1 |
| 2 |
(Ⅰ)求PO的长;
(Ⅱ)求二面角A-PM-C的正弦值.
考点:与二面角有关的立体几何综合题,点、线、面间的距离计算
专题:空间位置关系与距离,空间角
分析:(Ⅰ)连接AC,BD,以O为坐标原点,OA,OB,OP方向为x,y,z轴正方向建立空间坐标系O-xyz,分别求出向量
,
的坐标,进而根据MP⊥AP,得到
•
=0,进而求出PO的长;
(Ⅱ)求出平面APM和平面PMC的法向量,代入向量夹角公式,求出二面角的余弦值,进而根据平方关系可得:二面角A-PM-C的正弦值.
| AP |
| MP |
| AP |
| MP |
(Ⅱ)求出平面APM和平面PMC的法向量,代入向量夹角公式,求出二面角的余弦值,进而根据平方关系可得:二面角A-PM-C的正弦值.
解答:
解:(Ⅰ)连接AC,BD,
∵底面是以O为中心的菱形,PO⊥底面ABCD,
故AC∩BD=O,且AC⊥BD,
以O为坐标原点,OA,OB,OP方向为x,y,z轴正方向建立空间坐标系O-xyz,

∵AB=2,∠BAD=
,
∴OA=AB•cos(
∠BAD)=
,OB=AB•sin(
∠BAD)=1,
∴O(0,0,0),A(
,0,0),B(0,1,0),C(-
,0,0),
=(0,1,0),
=(-
,-1,0),
又∵BM=
,
∴
=
=(-
,-
,0),
则
=
+
=(-
,
,0),
设P(0,0,a),则
=(-
,0,a),
=(
,-
,a),
∵MP⊥AP,
∴
•
=
-a2=0,
解得a=
,
即PO的长为
.
(Ⅱ)由(Ⅰ)知
=(-
,0,
),
=(
,-
,
),
=(
,0,
),
设平面APM的法向量
=(x,y,z),平面PMC的法向量为
=(a,b,c),
由
,得
,
令x=1,则
=(1,
,2),
由
,得
,
令a=1,则
=(1,-
,-2),
∵平面APM的法向量
和平面PMC的法向量
夹角θ满足:
cosθ=
=
=-
故sinθ=
=
∵底面是以O为中心的菱形,PO⊥底面ABCD,
故AC∩BD=O,且AC⊥BD,
以O为坐标原点,OA,OB,OP方向为x,y,z轴正方向建立空间坐标系O-xyz,

∵AB=2,∠BAD=
| π |
| 3 |
∴OA=AB•cos(
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
∴O(0,0,0),A(
| 3 |
| 3 |
| OB |
| BC |
| 3 |
又∵BM=
| 1 |
| 2 |
∴
| BM |
| 1 |
| 4 |
| BC |
| ||
| 4 |
| 1 |
| 4 |
则
| OM |
| OB |
| BM |
| ||
| 4 |
| 3 |
| 4 |
设P(0,0,a),则
| AP |
| 3 |
| MP |
| ||
| 4 |
| 3 |
| 4 |
∵MP⊥AP,
∴
| AP |
| MP |
| 3 |
| 4 |
解得a=
| ||
| 2 |
即PO的长为
| ||
| 2 |
(Ⅱ)由(Ⅰ)知
| AP |
| 3 |
| ||
| 2 |
| MP |
| ||
| 4 |
| 3 |
| 4 |
| ||
| 2 |
| CP |
| 3 |
| ||
| 2 |
设平面APM的法向量
| m |
| n |
由
|
|
令x=1,则
| m |
5
| ||
| 3 |
由
|
|
令a=1,则
| n |
| 3 |
∵平面APM的法向量
| m |
| n |
cosθ=
| ||||
|
|
| 1-5-4 | ||||||
|
| ||
| 5 |
故sinθ=
| 1-cos2θ |
| ||
| 5 |
点评:本题考查的知识点是空间二面角的平面角,建立空间坐标系,将二面角问题转化为向量夹角问题,是解答的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 正方体ABCD-A1B1C1D1的8个顶点中任取4个连接构成的三棱锥中,满足任意一条棱都不与其表面垂直的三棱锥的个数( )
正方体ABCD-A1B1C1D1的8个顶点中任取4个连接构成的三棱锥中,满足任意一条棱都不与其表面垂直的三棱锥的个数( )| A、22 | B、24 | C、26 | D、28 |
下列函数中既是奇函数,又在区间(0,+∞)上单调递减的函数是( )
A、y=
| ||||
B、y=
| ||||
C、y=
| ||||
D、y=
|
 一同学为研究函数f(x)=
一同学为研究函数f(x)=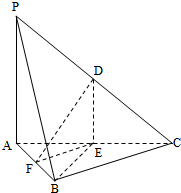 如图,在三棱锥P-ABC中,D,E,F分别为棱PC,AC,AB的中点,已知PA⊥AC,PA=6,BC=8,DF=5.求证:
如图,在三棱锥P-ABC中,D,E,F分别为棱PC,AC,AB的中点,已知PA⊥AC,PA=6,BC=8,DF=5.求证: 如图,已知二面角α-MN-β的大小为60°,菱形ABCD在面β内,A、B两点在棱MN上,∠BAD=60°,E是AB的中点,DO⊥面α,垂足为O.
如图,已知二面角α-MN-β的大小为60°,菱形ABCD在面β内,A、B两点在棱MN上,∠BAD=60°,E是AB的中点,DO⊥面α,垂足为O.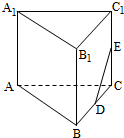 在如图所示的多面体中,四边形ABB1A1和ACC1A1都为矩形
在如图所示的多面体中,四边形ABB1A1和ACC1A1都为矩形