题目内容
已知变量x，y满足约束条件
，且有无穷多个点（x，y）使目标函数z=y+x取得最小值，则k=（ ）
|
| A、4 | B、3 | C、2 | D、1 |
考点：简单线性规划
专题：不等式的解法及应用
分析：作出不等式组对应的平面区域，利用目标函数的几何意义，即可确定目标函数z=x+y取得最小值的等价条件．
解答：
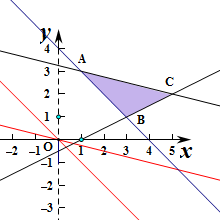解：作出不等式组对应的平面区域如图：（阴影部分ABC）．
直线kx+y-4=0过定点（0，4），
由z=x+y得y=-x+z，平移直线y=-x+z，
要使有无穷多个点（x，y）使得目标函数z=x+y取得最小值，
则目标函数y=-x+z和直线kx+y-4=0平行，
即两条直线的斜率相等即-k=-1，
解得k=1，
故选：D．
解：作出不等式组对应的平面区域如图：（阴影部分ABC）．直线kx+y-4=0过定点（0，4），
由z=x+y得y=-x+z，平移直线y=-x+z，
要使有无穷多个点（x，y）使得目标函数z=x+y取得最小值，
则目标函数y=-x+z和直线kx+y-4=0平行，
即两条直线的斜率相等即-k=-1，
解得k=1，
故选：D．
点评：本题主要考查线性规划的应用，利用目标函数的几何意义，结合数形结合的数学思想是解决此类问题的基本方法．
练习册系列答案
优生乐园系列答案
相关题目
已知正项等比数列{an}满足：a7=a6+2a5，若存在两项am，an，使得aman=16a12，则
+
的最小值为（ ）
| 1 |
| m |
| 4 |
| n |
A、
| ||
B、
| ||
C、
| ||
| D、不存在 |
正方体ABCD-A1B1C1D1的8个顶点中任取4个连接构成的三棱锥中，满足任意一条棱都不与其表面垂直的三棱锥的个数（ ）| A、22 | B、24 | C、26 | D、28 |
设一组数据31，37，33，a，35的平均数是34，则这组数据的方差是（ ）
| A、2.5 | B、3 | C、3.5 | D、4 |
已知函数f（x）=
，则f（f（2014））=（ ）
|
A、
| ||
B、-
| ||
| C、1 | ||
| D、-1 |
若x，y满足约束条件
，则
的最小值为（ ）
|
| x |
| y |
A、
| ||
B、
| ||
| C、1 | ||
D、
|
下列函数中既是奇函数，又在区间（0，+∞）上单调递减的函数是（ ）
A、y=
| ||||
B、y=
| ||||
C、y=
| ||||
D、y=
|