题目内容
已知函数f(x)=π(x-cosx)-2sinx-2,g(x)=(x-π)
+
-1.
证明:
(Ⅰ)存在唯一x0∈(0,
),使f(x0)=0;
(Ⅱ)存在唯一x1∈(
,π),使g(x1)=0,且对(Ⅰ)中的x0,有x0+x1>π.
|
| 2x |
| π |
证明:
(Ⅰ)存在唯一x0∈(0,
| π |
| 2 |
(Ⅱ)存在唯一x1∈(
| π |
| 2 |
考点:函数零点的判定定理
专题:函数的性质及应用,导数的概念及应用
分析:(Ⅰ)导数法可判f(x)在(0,
)上为增函数,又可判函数有零点,故必唯一;(Ⅱ)化简可得g(x)=(π-x)
+
-1,换元法,令t=π-x,记u(t)=g(π-t)=-
-
t+1,t∈[0,
],由导数法可得函数的零点,可得不等式.
| π |
| 2 |
| cosx |
| 1+sinx |
| 2x |
| π |
| tcost |
| 1+sint |
| 2 |
| π |
| π |
| 2 |
解答:
解:(Ⅰ)当x∈(0,
)时,f′(x)=π+πsinx-2cosx>0,
∴f(x)在(0,
)上为增函数,
又f(0)=-π-2<0,f(
)=
-4>0,
∴存在唯一x0∈(0,
),使f(x0)=0;
(Ⅱ)当x∈[
,π]时,
化简可得g(x)=(x-π)
+
-1
=(π-x)
+
-1,
令t=π-x,记u(t)=g(π-t)=-
-
t+1,t∈[0,
],
求导数可得u′(t)=
,
由(Ⅰ)得,当t∈(0,x0)时,u′(t)<0,当t∈(x0,
)时,u′(t)>0,
∴函数u(t)在(x0,
)上为增函数,
由u(
)=0知,当t∈[x0,
)时,u(t)<0,
∴函数u(t)在[x0,
)上无零点;
函数u(t)在(0,x0)上为减函数,
由u(0)=1及u(x0)<0知存在唯一t0∈(0,x0),使u(t0)=0,
于是存在唯一t0∈(0,
),使u(t0)=0,
设x1=π-t0∈(
,π),则g(x1)=g(π-t0)=u(t0)=0,
∴存在唯一x1∈(
,π),使g(x1)=0,
∵x1=π-t0,t0<x0,
∴x0+x1>π
| π |
| 2 |
∴f(x)在(0,
| π |
| 2 |
又f(0)=-π-2<0,f(
| π |
| 2 |
| π2 |
| 2 |
∴存在唯一x0∈(0,
| π |
| 2 |
(Ⅱ)当x∈[
| π |
| 2 |
化简可得g(x)=(x-π)
|
| 2x |
| π |
=(π-x)
| cosx |
| 1+sinx |
| 2x |
| π |
令t=π-x,记u(t)=g(π-t)=-
| tcost |
| 1+sint |
| 2 |
| π |
| π |
| 2 |
求导数可得u′(t)=
| f(t) |
| π(1+sint) |
由(Ⅰ)得,当t∈(0,x0)时,u′(t)<0,当t∈(x0,
| π |
| 2 |
∴函数u(t)在(x0,
| π |
| 2 |
由u(
| π |
| 2 |
| π |
| 2 |
∴函数u(t)在[x0,
| π |
| 2 |
函数u(t)在(0,x0)上为减函数,
由u(0)=1及u(x0)<0知存在唯一t0∈(0,x0),使u(t0)=0,
于是存在唯一t0∈(0,
| π |
| 2 |
设x1=π-t0∈(
| π |
| 2 |
∴存在唯一x1∈(
| π |
| 2 |
∵x1=π-t0,t0<x0,
∴x0+x1>π
点评:本题考查零点的判定定理,涉及导数法证明函数的单调性,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列函数中既是奇函数,又在区间(0,+∞)上单调递减的函数是( )
A、y=
| ||||
B、y=
| ||||
C、y=
| ||||
D、y=
|
已知a,b是正数,且a+b=1,则
+
( )
| 1 |
| a |
| 4 |
| b |
| A、有最小值8 |
| B、有最小值9 |
| C、有最大值8 |
| D、有最大值9 |
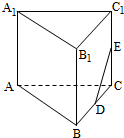 在如图所示的多面体中,四边形ABB1A1和ACC1A1都为矩形
在如图所示的多面体中,四边形ABB1A1和ACC1A1都为矩形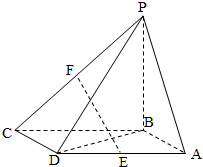 如图,四棱锥P-ABCD的底面ABCD是平行四边形,BA=BD=
如图,四棱锥P-ABCD的底面ABCD是平行四边形,BA=BD=