题目内容
已知函数f(x)=a-
.
(Ⅰ)若函数f(x)为奇函数,求a的值;
(Ⅱ)若a=2,则是否存在实数m,n(m<n<0),使得函数f(x)的定义域和值域都为[m,n]?若存在,求出m,n的值;若不存在,请说明理由.
| 2 |
| 2x+1 |
(Ⅰ)若函数f(x)为奇函数,求a的值;
(Ⅱ)若a=2,则是否存在实数m,n(m<n<0),使得函数f(x)的定义域和值域都为[m,n]?若存在,求出m,n的值;若不存在,请说明理由.
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:(Ⅰ)函数f(x)为奇函数,且定义域为R,由f(0)=0求a的值;
(Ⅱ)把a=2代入函数解析式,假设存在实数m、n(m<n<0)满足题意,则有
,即m、n是方程
f(x)=x的两个不等负根,然后分析方程2-
=x无负根说明假设错误.
(Ⅱ)把a=2代入函数解析式,假设存在实数m、n(m<n<0)满足题意,则有
|
f(x)=x的两个不等负根,然后分析方程2-
| 2 |
| 2x+1 |
解答:
解:(Ⅰ)∵f(x)为R上的奇函数,
∴f(0)=0,即a-1=0,a=1;
(Ⅱ)不存在实数m、n满足题意.
当a=2时,f(x)=2-
,
∵y=2x在R上是增函数,∴f(x)在R上是增函数.
假设存在实数m、n(m<n<0)满足题意,则有
,
即m、n是方程f(x)=x的两个不等负根.
由2-
=x,得2x+1=-
.
令h(x)=2x+1,g(x)=-
.
∵函数g(x)在(-∞,0]上单调递增,
∴当x<0时,g(x)<g(0)=1.
而h(x)>1,∴h(x)>g(x),
∴方程2x+1=-
在(-∞,0)上无解.
故不存在实数m、n满足题意.
∴f(0)=0,即a-1=0,a=1;
(Ⅱ)不存在实数m、n满足题意.
当a=2时,f(x)=2-
| 2 |
| 2x+1 |
∵y=2x在R上是增函数,∴f(x)在R上是增函数.
假设存在实数m、n(m<n<0)满足题意,则有
|
即m、n是方程f(x)=x的两个不等负根.
由2-
| 2 |
| 2x+1 |
| 2 |
| x-2 |
令h(x)=2x+1,g(x)=-
| 2 |
| x-2 |
∵函数g(x)在(-∞,0]上单调递增,
∴当x<0时,g(x)<g(0)=1.
而h(x)>1,∴h(x)>g(x),
∴方程2x+1=-
| 2 |
| x-2 |
故不存在实数m、n满足题意.
点评:本题考查了函数奇偶性的判断,考查了由函数的单调性求函数的值域,训练了存在性问题的证明方法,是中档题.

练习册系列答案
相关题目
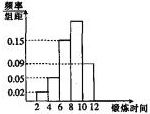 某校友200位教职员工,其每周用于锻炼身体所用时间的频率分布直方图如图所示,据图估计,锻炼时间在[8,10]小时内的人数为( )
某校友200位教职员工,其每周用于锻炼身体所用时间的频率分布直方图如图所示,据图估计,锻炼时间在[8,10]小时内的人数为( )| A、76 | B、82 | C、88 | D、95 |
已知在等差数列{an}中,对任意正整数n,都有an>an+1,且a2,a8是方程x2-12x+m=0的两根,且前15项的和为5m,则数列{an}的公差是( )
| A、-2或-3 | B、2或3 |
| C、-2 | D、-3 |
定义在R上的函数f(x),当x≠-2时,恒有(x+2)f′(x)<0(其中f′(x)是函数f(x)的导数),又a=f(log
3),b=f[(
)0.1],c=f(ln3),则( )
| 1 |
| 3 |
| 1 |
| 3 |
| A、a<b<c |
| B、b<c<a |
| C、c<a<b |
| D、c<b<a |