题目内容
15．设复数z满足z（l+i）=3-i，则|$\overline{z}$|等于（ ）| A． | $\sqrt{5}$ | B． | 5 | C． | 1-2i | D． | 1+2i |
分析 把已知等式变形，再由复数代数形式的乘除运算化简复数z，求出$\overline{z}$，再由复数求模公式计算得答案．
解答 解：由z（l+i）=3-i，
得$z=\frac{3-i}{1+i}=\frac{（3-i）（1-i）}{（1+i）（1-i）}=\frac{2-4i}{2}=1-2i$．
∴$\overline{z}=1+2i$．
∴|$\overline{z}$|=$\sqrt{1+{2}^{2}}=\sqrt{5}$．
故选：A．
点评 本题考查复数代数形式的乘除运算，考查了复数模的求法，是基础题．
练习册系列答案
阅读快车系列答案
相关题目
6．设向量$\overrightarrow{a}$，$\overrightarrow{b}$是互相垂直的两个单位向量，且|$\overrightarrow{a}$-3$\overrightarrow{b}$|=m|$\overrightarrow{a}$+$\overrightarrow{b}$|，则实数m的值为（ ）
| A． | $\sqrt{10}$ | B． | ±$\sqrt{10}$ | C． | $\sqrt{5}$ | D． | ±$\sqrt{5}$ |
3．
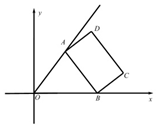已知射线OP：y=$\frac{4}{3}$x（x≥0）和矩形ABCD，AB=16，AD=9，点A、B分别在射线OP和x轴非负半轴上，则线段OD长度的最大值为（ ）
已知射线OP：y=$\frac{4}{3}$x（x≥0）和矩形ABCD，AB=16，AD=9，点A、B分别在射线OP和x轴非负半轴上，则线段OD长度的最大值为（ ）| A． | $\sqrt{337}$ | B． | 27 | C． | $\sqrt{689}$ | D． | 29 |
7．已知函数y=$\frac{1}{2}$x2的图象在点（x0，$\frac{1}{2}$x02）处的切线为l，若l也为函数y=lnx（0＜x＜1）的图象的切线，则x0必须满足（ ）
| A． | $\frac{\sqrt{2}}{2}$＜x0＜1 | B． | 1＜x0＜$\sqrt{2}$ | C． | $\sqrt{2}$＜x0＜$\sqrt{3}$ | D． | $\sqrt{3}$＜x0＜2 |
4．已知集合A={1，2，3}，$B=\left\{{x|\frac{2-x}{x}≥0}\right\}$，则A∩B=（ ）
| A． | {0，1，2} | B． | {1，2} | C． | {2，3} | D． | {0，2，3} |
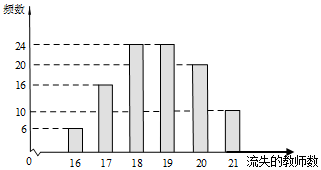2017年两会继续关注了乡村教师的问题，随着城乡发展失衡，乡村教师待遇得不到保障，流失现象严重，教师短缺会严重影响乡村孩子的教育问题，为此，某市今年要为某所乡村中学招聘储备未来三年的教师，现在每招聘一名教师需要2万元，若三年后教师严重短缺时再招聘，由于各种因素，则每招聘一名教师需要5万元，已知现在该乡村中学无多余教师，为决策应招聘多少乡村教师搜集并整理了该市100所乡村中学在过去三年内的教师流失数，得到右面的柱状图：记x表示一所乡村中学在过去三年内流失的教师数，y表示一所乡村中学未来四年内在招聘教师上所需的费用（单位：万元），n表示今年为该乡村中学招聘的教师数，为保障乡村孩子教育不受影响，若未来三年内教师有短缺，则第四年马上招聘