题目内容

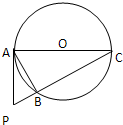
如图，PA是圆O的切线，A为切点，PA=4，PB=2，则直径AC=
 
．
考点：与圆有关的比例线段
专题：立体几何
分析：因为PA切圆O于A，由切割线定理得：PA2=PB×PC，所以在Rt△PAC中，算出AC=
PC2-PA2
，进而得到答案．
解答： 解：∵PA切圆O于A，PA=4，PB=2，
由切割线定理得：PA2=PB×PC，
∴PC=8，
在Rt△PAC中，算出AC=
PC2-PA2
=4
3
，
故答案为：4
3
点评：本题给出圆的切线PA、割线PC和圆的直径AC，求线段PB的长，着重考查了圆的切线的性质和与圆有关的比例线段等知识，属于基础题．
练习册系列答案
相关题目
已知函数f（x）=
1
4
（x+1）2，若存在t∈R，只要x∈[1，m]（m＞1），就有f（x+t）≤x，则m的最大值是
 
．
已知实数x，y满足xy+2x+3y-3=0．
（1）若x，y∈R，则x+y的取值范围是
 
；
（2）若x，y∈R+，则x+y的取值范围是
 
．
设抛物线W：y2=4x的焦点为F，过F的直线与W相交于A，B两点，记点F到直线l：x=-1的距离为d，则有（　　）
A、|AB|≥2d
B、|AB|=2d
C、|AB|≤2d
D、|AB|＜2d
设A={x，y}，B={1，xy}，若A=B，求x，y分别为
 
．
函数f（x）=ln（x+2）-
1
x
的零点所在区间为（k，k+1）（其中k为整数），则k的值为（　　）
A、0B、1C、-2D、0或-2
已知双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）的两条渐近线与抛物线y2=2px（p＞0）的准线分别交于A、B两点，O为坐标原点，若双曲线的离心率为2，△AOB的面积为
3
，则该抛物线的标准方程是
 
．
函数f（x）=x3-x2+ax+b在点x=1处的切线与直线y=2x+1垂直，则a=
 
．
双曲线上右支上存在点P，使得右焦点F关于直线OP的对称点在y轴上（O为坐标原点），则双曲线离心率的取值范围为（　　）
A、(
2
，
3
)
B、(
2
，+∞)
C、(1，
2
)
D、(
3
，+∞)

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网