题目内容
设抛物线W:y2=4x的焦点为F,过F的直线与W相交于A,B两点,记点F到直线l:x=-1的距离为d,则有( )
| A、|AB|≥2d |
| B、|AB|=2d |
| C、|AB|≤2d |
| D、|AB|<2d |
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:由抛物线方程求出F的坐标,得到F到准线l的距离d=2,设出过焦点的直线方程,和抛物线联立后利用根与系数的关系求出焦点弦的长度,然后核对四个选项得答案.
解答:
解:如图,设A(x1,y1),B(x2,y2),
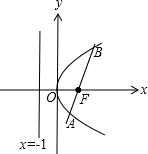
由抛物线W:y2=4x,得焦点为F(1,0),准线l:x=-1.
F到准线的距离d=2.
设直线AB的方程为x=ty+1,
联立
,得y1+y2=4t.
x1+x2=t(y1+y2)+2=4t2+2≥2.
则|AB|=x1+x2+2≥4=2d.
故选:A.

由抛物线W:y2=4x,得焦点为F(1,0),准线l:x=-1.
F到准线的距离d=2.
设直线AB的方程为x=ty+1,
联立
|
x1+x2=t(y1+y2)+2=4t2+2≥2.
则|AB|=x1+x2+2≥4=2d.
故选:A.
点评:本题考查了抛物线的简单几何性质,考查了数学转化思想方法,是基础题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
下列函数满足性质:“f(-x)=f(x)”的函数是( )
| A、f(x)=x-1 |
| B、f(x)=-x2+x |
| C、f(x)=2x-2-x |
| D、f(x)=2x+2-x |
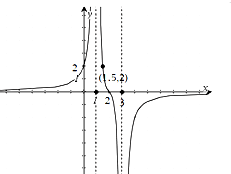 已知函数y=f(x)的图象(如图所示)过点(0,2)、(1.5,2)和点(2,0),且函数图象关于点(2,0)对称;直线x=1和x=3及y=0是它的渐近线.现要求根据给出的函数图象研究函数g(x)=
已知函数y=f(x)的图象(如图所示)过点(0,2)、(1.5,2)和点(2,0),且函数图象关于点(2,0)对称;直线x=1和x=3及y=0是它的渐近线.现要求根据给出的函数图象研究函数g(x)=