题目内容
函数f（x）=x3-x2+ax+b在点x=1处的切线与直线y=2x+1垂直，则a= ．
考点：利用导数研究曲线上某点切线方程
专题：计算题,导数的概念及应用,直线与圆
分析：由题意求导f′（x）=3x2-2x+a，由垂直知斜率之积为-1，即f′（1）•2=-1，从而解得．
解答：
解：由题意，
f′（x）=3x2-2x+a，
∵函数f（x）=x3-x2+ax+b在点x=1处的切线与直线y=2x+1垂直，
∴f′（1）•2=-1；
故（3-2+a）•2=-1；
解得，a=-
；
故答案为：-
．
f′（x）=3x2-2x+a，
∵函数f（x）=x3-x2+ax+b在点x=1处的切线与直线y=2x+1垂直，
∴f′（1）•2=-1；
故（3-2+a）•2=-1；
解得，a=-
| 3 |
| 2 |
故答案为：-
| 3 |
| 2 |
点评：本题考查了导数的求法及其几何意义，同时考查了直线与直线位置关系的应用，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
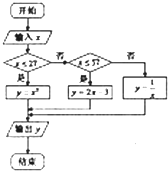若程序框图如图所示，视x为自变量，y为函数值，可得函数y=f（x）的解析式，那么函数f（x）-4在x∈R上的零点个数为（ ）