题目内容
已知双曲线
-
=1(a>0,b>0)的两条渐近线与抛物线y2=2px(p>0)的准线分别交于A、B两点,O为坐标原点,若双曲线的离心率为2,△AOB的面积为
,则该抛物线的标准方程是 .
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
考点:双曲线的简单性质
专题:
分析:把x=-
代入y=±
x,解得y,可得|AB|=
,利用△AOB的面积为
,可得
×
×
=
,再利用e=
=
=2,解得
.即可得出p.
| p |
| 2 |
| b |
| a |
| pb |
| a |
| 3 |
| 1 |
| 2 |
| p |
| 2 |
| pb |
| a |
| 3 |
| c |
| a |
1+(
|
| b |
| a |
解答:
解:把x=-
代入y=±
x,解得y=±
.
∴|AB|=
,
∵△AOB的面积为
,
∴
×
×
=
,
由e=
=
=2,解得
=
.
∴
×
=
,
解得p=2.
∴该抛物线的标准方程是y2=4x.
故答案为:y2=4x.
| p |
| 2 |
| b |
| a |
| pb |
| 2a |
∴|AB|=
| pb |
| a |
∵△AOB的面积为
| 3 |
∴
| 1 |
| 2 |
| p |
| 2 |
| pb |
| a |
| 3 |
由e=
| c |
| a |
1+(
|
| b |
| a |
| 3 |
∴
| p2 |
| 4 |
| 3 |
| 3 |
解得p=2.
∴该抛物线的标准方程是y2=4x.
故答案为:y2=4x.
点评:本题考查了双曲线与抛物线的标准方程及其性质,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
设F1,F2为双曲线C:
-
=1(a>0,b>0)的左、右焦点,且直线y=2x为双曲线C的一条渐近线,点P为C上一点,如果|PF1|-|PF2|=4,那么双曲线C的方程为 ;离心率为 .
| x2 |
| a2 |
| y2 |
| b2 |
方程f(x)=x的根称为f(x)的不动点,若函数f(x)=
有唯一不动点,且x1=1000,xn+1=
(n∈N*),则x2013=( )
| x |
| a(x+2) |
| 1 | ||
f(
|
| A、2006 | B、2008 |
| C、2012 | D、2013 |
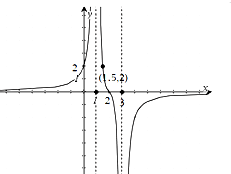 已知函数y=f(x)的图象(如图所示)过点(0,2)、(1.5,2)和点(2,0),且函数图象关于点(2,0)对称;直线x=1和x=3及y=0是它的渐近线.现要求根据给出的函数图象研究函数g(x)=
已知函数y=f(x)的图象(如图所示)过点(0,2)、(1.5,2)和点(2,0),且函数图象关于点(2,0)对称;直线x=1和x=3及y=0是它的渐近线.现要求根据给出的函数图象研究函数g(x)=
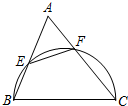 如图,在△ABC中,以BC为直径的半圆分别交AB,AC于点E,F,且AC=2AE,那么
如图,在△ABC中,以BC为直径的半圆分别交AB,AC于点E,F,且AC=2AE,那么