题目内容
已知实数x，y满足xy+2x+3y-3=0．
（1）若x，y∈R，则x+y的取值范围是 ；
（2）若x，y∈R+，则x+y的取值范围是 ．
（1）若x，y∈R，则x+y的取值范围是
（2）若x，y∈R+，则x+y的取值范围是
考点：一元二次不等式的应用
专题：不等式的解法及应用
分析：（1）令u=x+y，则y=u-x，代入xy+2x+3y-3=0．化为x2+（1-u）x+3-3u=0，由于x∈R，可得△≥0，解出即可．
（2）由实数x，y满足xy+2x+3y-3=0．可得y=
＞0，解得0＜x＜
．因此x+y=x+
=x-
+2=f（x），利用导数研究其单调性极值即可得出．
（2）由实数x，y满足xy+2x+3y-3=0．可得y=
| 3-2x |
| x+3 |
| 3 |
| 2 |
| 3-2x |
| x+3 |
| 3 |
| x+3 |
解答：
解：（1）令u=x+y，则y=u-x，
∵实数x，y满足xy+2x+3y-3=0．
∴x（u-x）+2x+3（u-x）-3=0，
化为x2+（1-u）x+3-3u=0，
∵x∈R，
∴△≥0，
化为u2+10u-11≥0，
解得u≤-11，或u≥1．
∴x+y的取值范围是（-∞，-11]∪[1，+∞）．
（2）∵实数x，y满足xy+2x+3y-3=0．
∴y=
＞0，解得0＜x＜
．
∴x+y=x+
=x-
+2=f（x），
f′（x）=1+
＞0，
∴函数f（x）在(0，
)上单调递增．
∴f(0)＜f(x)＜f(
)，
即1＜f（x）＜
．
∴x+y的取值范围是(1，
)．
故答案分别为：（-∞，-11]∪[1，+∞），(1，
)．．
∵实数x，y满足xy+2x+3y-3=0．
∴x（u-x）+2x+3（u-x）-3=0，
化为x2+（1-u）x+3-3u=0，
∵x∈R，
∴△≥0，
化为u2+10u-11≥0，
解得u≤-11，或u≥1．
∴x+y的取值范围是（-∞，-11]∪[1，+∞）．
（2）∵实数x，y满足xy+2x+3y-3=0．
∴y=
| 3-2x |
| x+3 |
| 3 |
| 2 |
∴x+y=x+
| 3-2x |
| x+3 |
| 3 |
| x+3 |
f′（x）=1+
| 3 |
| (x+3)2 |
∴函数f（x）在(0，
| 3 |
| 2 |
∴f(0)＜f(x)＜f(
| 3 |
| 2 |
即1＜f（x）＜
| 17 |
| 6 |
∴x+y的取值范围是(1，
| 17 |
| 6 |
故答案分别为：（-∞，-11]∪[1，+∞），(1，
| 17 |
| 6 |
点评：本题考查了一元二次方程有实数根与判别式的关系、利用导数研究函数的单调性极值，考查了推理能力与计算能力，属于难题．
练习册系列答案
相关题目
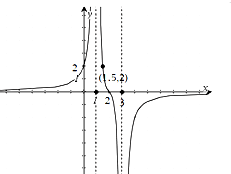已知函数y=f（x）的图象（如图所示）过点（0，2）、（1.5，2）和点（2，0），且函数图象关于点（2，0）对称；直线x=1和x=3及y=0是它的渐近线．现要求根据给出的函数图象研究函数g（x）=