题目内容
解方程：（6x-5）[1+
]+x（1+
）=0．
| (6x-5)2+4 |
| x2+4 |
考点：根式与分数指数幂的互化及其化简运算
专题：转化思想
分析：原式可化为：（6x-5）[1+
]=-x（1+
），设t=6x-5，即有t（1+
）与x（1+
）形式一样，故只需要6x-5=-x即可得解．
| (6x-5)2+4 |
| x2+4 |
| t2+4 |
| x2+4 |
解答：
解：（6x-5）[1+
]+x（1+
）=0．
即：（6x-5）[1+
]=-x（1+
）
由于方程形式可知，设t=6x-5
即有t（1+
）与x（1+
）形式一样，
故只需要满足 6x-5=-x即可，
解得：x=
．
| (6x-5)2+4 |
| x2+4 |
即：（6x-5）[1+
| (6x-5)2+4 |
| x2+4 |
由于方程形式可知，设t=6x-5
即有t（1+
| t2+4 |
| x2+4 |
故只需要满足 6x-5=-x即可，
解得：x=
| 5 |
| 7 |
点评：本题考查了转化思想，考察了探究能力，属于基础题．
练习册系列答案
阳光课堂同步练习系列答案
相关题目
已知函数f（x+1）=x2+2x-1，x∈[1，2]，则f（x）是（ ）
| A、[1，2]上的增函数 |
| B、[1，2]上的减函数 |
| C、[2，3]上的增函数 |
| D、[2，3]上的减函数 |
已知复数z满足|（1-i）z=i2014（其中i为虚数单位），则
的虚部为（ ）
. |
| z |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
如图，在底面为平行四边形的四棱锥P-ABCD中，AB⊥AC，PA⊥平面ABCD，且PA=AB，点E是PD的中点．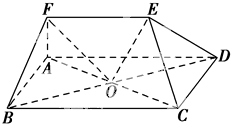
在多面体ABCDEF中，点O是矩形ABCD的对角线的交点，三角形CDE是等边三角形，棱EF∥BC且EF=