题目内容
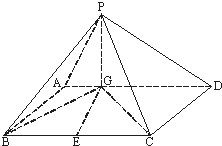如图四棱锥P-ABCD中，底面ABCD是平行四边形，PG⊥平面ABCD，垂足为G，G在AD上且AG=| 1 |
| 3 |
| 8 |
| 3 |
（1）求过点P，C，B，G四点的球的表面积；
（2）求直线DP与平面PBG所成角的正弦值．
考点：直线与平面所成的角
专题：空间位置关系与距离,空间角
分析：（1）首先利用四面体的体积公式求出PG的长，再以GP，GB，GC构造长方体，外接球的直径为长方体的对角线，求出R，进一步确定表面积．
（2）先做出直线与平面的夹角进一步求出结果．
（2）先做出直线与平面的夹角进一步求出结果．
解答：
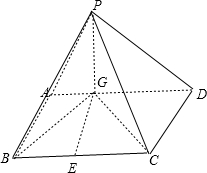解：（1）四棱锥P-ABCD中，PG⊥平面ABCD
∵四面体P-BCG的体积为
．
∴
•
BG•GC•PG=
∵GB=GC=2，
解得：PG=4
以GP，GB，GC构造长方体，外接球的直径为长方体的对角线，
所以：（2R）2=16+4+4
解得：R=
S=4πR2=24π
（2）由GB=GC=2
∴△BGC为等腰三角形，
GE为∠BGC的角平分线，作DK⊥BG交BG的延长线于K，
∴DK⊥平面BGP．
由平面几何知识可知：DK=GK=
，PD=
设直线DP与平面PBG所成角为α
∴sinα=
=
解：（1）四棱锥P-ABCD中，PG⊥平面ABCD∵四面体P-BCG的体积为
| 8 |
| 3 |
∴
| 1 |
| 3 |
| 1 |
| 2 |
| 8 |
| 3 |
∵GB=GC=2，
解得：PG=4
以GP，GB，GC构造长方体，外接球的直径为长方体的对角线，
所以：（2R）2=16+4+4
解得：R=
| 6 |
S=4πR2=24π
（2）由GB=GC=2
∴△BGC为等腰三角形，
GE为∠BGC的角平分线，作DK⊥BG交BG的延长线于K，
∴DK⊥平面BGP．
由平面几何知识可知：DK=GK=
| 3 |
| 2 |
|
设直线DP与平面PBG所成角为α
∴sinα=
| DK |
| DP |
3
| ||
| 82 |
点评：本题考查的知识要点：几何体的体积公式和表面积公式的应用，线面夹角的应用．
练习册系列答案
相关题目
如图，在底面为平行四边形的四棱锥P-ABCD中，AB⊥AC，PA⊥平面ABCD，且PA=AB，点E是PD的中点．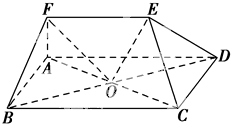
在多面体ABCDEF中，点O是矩形ABCD的对角线的交点，三角形CDE是等边三角形，棱EF∥BC且EF=