题目内容
下列命题中正确的是( )
| A、若a>b,则ac2>bc2 | ||||
B、若a>b,c<d,则
| ||||
| C、若a>b,c>d,则a-c>b-d | ||||
D、若ab>0,a>b,则
|
考点:不等式的基本性质
专题:不等式的解法及应用
分析:由不等式的性质逐个选项验证可得.
解答:
解:选项A,当a>b时,取c=0,则ac2>bc2不成立,故错误;
选项B,取a=d=1,b=0,c=-1,可得
=-1,
=0,显然
>
不成立,故错误;
选项C,取a=2,b=1,c=2,d=1,显然有a-c=b-d,故错误;
选项D,∵ab>0,a>b,∴由不等式的性质可得
>
,即
<
,故正确.
故选:D
选项B,取a=d=1,b=0,c=-1,可得
| a |
| c |
| b |
| d |
| a |
| c |
| b |
| d |
选项C,取a=2,b=1,c=2,d=1,显然有a-c=b-d,故错误;
选项D,∵ab>0,a>b,∴由不等式的性质可得
| a |
| ab |
| b |
| ab |
| 1 |
| a |
| 1 |
| b |
故选:D
点评:本题考查不等式的性质,属基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列各列数都是依照一定的规律排列,在括号里填上适当的数2,3,5,8,12,( )
| A、20 | B、19 | C、18 | D、17 |
参数方程
(θ为参数)化为普通方程是( )
|
| A、2x-y+1=0 |
| B、2x+y-1=0 |
| C、2x-y+1=0,x∈[0,1] |
| D、2x+y-1=0,x∈[0,1] |
已知数列{an}满足a1=0,an+1=an+2n(n∈N*),那么a2011的值是( )
| A、2 0112 |
| B、2 012×2 011 |
| C、2 009×2 010 |
| D、2 010×2 011 |
 如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且PA=AB,点E是PD的中点.
如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且PA=AB,点E是PD的中点.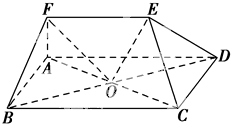 在多面体ABCDEF中,点O是矩形ABCD的对角线的交点,三角形CDE是等边三角形,棱EF∥BC且EF=
在多面体ABCDEF中,点O是矩形ABCD的对角线的交点,三角形CDE是等边三角形,棱EF∥BC且EF=