题目内容
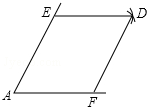如图，点E，F分别是锐角∠A两边上的点，AE=AF，分别以点E，F为圆心，以AE的长为半径画弧，两弧相交于点D，连接DE，DF．（1）请你判断所画四边形的性状，并说明理由；
（2）连接EF，若AE=8厘米，∠A=60°，求线段EF的长．
考点：进行简单的合情推理
专题：应用题
分析：（1）通过画图得出四边形AEDF是菱形；（2）由题意判断出△AEF是等边三角形，从而求出EF的长．
解答：
解：（1）通过画图得出：AE=ED=DF=AF，
∴四边形AEDF是菱形；
（2）∵∠A=60°，AE=AF，
∴△AEF是等边三角形，
∴EF=AE=8cm．
∴四边形AEDF是菱形；
（2）∵∠A=60°，AE=AF，
∴△AEF是等边三角形，
∴EF=AE=8cm．
点评：本题考查了菱形的判定，考查了菱形的性质，是一道基础题．
练习册系列答案
轻松课堂单元测试AB卷系列答案
小题狂做系列答案
相关题目
已知函数f（x）=
+
的两个极值点分别为x1，x2，且x1∈（0，1），x2∈（1，+∞），点P（m，n）表示的平面区域为D，若函数y=loga（x+4）（a＞1）的图象上存在区域D内的点，则实数a的取值范围为（ ）
| x3 |
| 3 |
| mx2+(m+n)x+1 |
| 2 |
| A、（1，3] |
| B、（1，3） |
| C、（3，+∞） |
| D、[3，+∞） |