题目内容

已知a＞0且a≠1，设f（x）=
ax
ax+
a
，求f（
1
10
）+f（
2
10
）+…+f（
9
10
）的值．
考点：函数的值
专题：函数的性质及应用
分析：由已知得f（x）+f（1-x）=
ax
ax+
a
+
a1-x
a1-x+
a
=
ax
ax+
a
+
a
a+ax×
a
=1，由此能求出f（
1
10
）+f（
2
10
）+…+f（
9
10
）的值．
解答： 解：∵a＞0且a≠1，f（x）=
ax
ax+
a
，
∴f（x）+f（1-x）=
ax
ax+
a
+
a1-x
a1-x+
a

=
ax
ax+
a
+
a
a+ax×
a
=1，
∴f（
1
10
）+f（
2
10
）+…+f（
9
10
）
=[f（
1
10
）+f（
9
10
）]+[f（
2
10
）+f（
8
10
）]+[f（
3
10
）+f（
7
10
）]+[f（
4
10
）+f（
6
10
）]+f（
5
10
）
=4+
a
a
+
a
=
9
2
．
点评：本题考查函数值的求法，是基础题，解题时要认真审题，注意函数性质的合理运用．
练习册系列答案
相关题目
已知数列{an}的通项公式an=
2n-3
2n
，求前n项和Sn．
已知A（-2，
3
），F是椭圆
x2
16
+
y2
12
=1的右焦点，点M在椭圆上，当|MA|+|MF|取得最小值时，点M的坐标为
 
．
已知椭圆
x2
a2
+
y2
b2
=1的离心率为
2
2
，且过点P（
2
2
，
1
2
），求椭圆的方程．
数列{an}的前n项和为Sn，若a1=1，an+1=3Sn，n∈N*，则a2014=
 
．
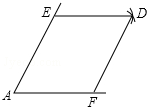如图，点E，F分别是锐角∠A两边上的点，AE=AF，分别以点E，F为圆心，以AE的长为半径画弧，两弧相交于点D，连接DE，DF．
（1）请你判断所画四边形的性状，并说明理由；
（2）连接EF，若AE=8厘米，∠A=60°，求线段EF的长．
已知抛物线y=ax2+bx+c与直线y=mx+n相交于两点，这两点的坐标分别是（0，-
1
2
）和（m-b，m2-mb+n），其中a，b，c，m，n为实数，且a，m不为0．
（1）求c的值；
（2）设抛物线y=ax2+bx+c与x轴的两个交点是（x1，0）和（x2，0），求x1x2的值；
（3）当-1≤x≤1时，设抛物线y=ax2+bx+c上与x轴距离最大的点为P（xo，yo ），
求这时|yo|的最小值．
若直线l过点A（0，a），斜率为1，圆x2+y2=4上恰有1个点到l的距离为1，则a的值为（　　）
A、3
2
B、±3
2
C、±2
D、±
2
求函数y=|x+3|+|x-5|的值域．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网