题目内容
已知函数f(x+1)是奇函数,则函数f(x)的图象的中心对称点是 .
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:由函数f(x+1)是奇函数,关于原点对称,函数f(x)的图象是由函数f(x+1)的图象向右移动一个单位得到了,即可得到中心对称点.
解答:
解:因为函数f(x+1)是奇函数,故图象关于原点对称,
函数f(x)的图象是由函数f(x+1)的图象向右移动一个单位得到了,
故函数f(x+1)的图象的中心对称点是(1,0).
故答案为:(1,0).
函数f(x)的图象是由函数f(x+1)的图象向右移动一个单位得到了,
故函数f(x+1)的图象的中心对称点是(1,0).
故答案为:(1,0).
点评:本题主要考查奇函数的性质和图象的对称性.

练习册系列答案
相关题目
若f(x)是奇函数,且x0是函数y=f(x)-ex的一个零点,则-x0一定是下列哪个函数的零点( )
| A、y=f(-x)ex-1 |
| B、y=f(x)e-x+1 |
| C、y=f(x)ex+1 |
| D、y=f(x)ex-1 |
已知一元二次函数f(x)=x2+bx+c,且不等式x2+bx+c>0的解集为{x|x<-1或x>
},则f(10x)>0的解集为( )
| 1 |
| 2 |
| A、{x|x<-1或x>lg2} |
| B、{x|-1<x<lg2} |
| C、{x|x>-lg2} |
| D、{x|x<-lg2} |
函数y=2x-x2的图象大致是( )
A、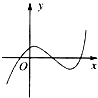 |
B、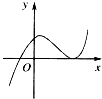 |
C、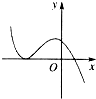 |
D、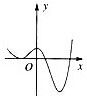 |
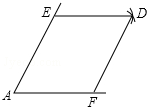 如图,点E,F分别是锐角∠A两边上的点,AE=AF,分别以点E,F为圆心,以AE的长为半径画弧,两弧相交于点D,连接DE,DF.
如图,点E,F分别是锐角∠A两边上的点,AE=AF,分别以点E,F为圆心,以AE的长为半径画弧,两弧相交于点D,连接DE,DF.