题目内容
函数f(x)为奇函数,且当x<0时,f(x)=x2+3x+2
(1)求x>0时,f(x)的解析式;
(2)当x∈[1,3]时,求f(x)的最值.
(1)求x>0时,f(x)的解析式;
(2)当x∈[1,3]时,求f(x)的最值.
考点:二次函数在闭区间上的最值,函数解析式的求解及常用方法
专题:函数的性质及应用
分析:由条件利用函数的奇偶性求出函数的解析式,再利用二次函数的性质求得f(x)在闭区间上的最值.
解答:
解:(1)设x>0,则-x<0,由题意可得f(-x)=(-x)2+3(-x)+2=x2-3x+2=-f(x),∴f(x)=-x2+3x-2.
再根据f(x)为奇函数,f(0)=0,可得f(x)=
.
(2)当x∈[1,3]时,由于二次函数f(x)在[1,
]上单调递增,在[
,3]上单调递减,
故当x=
时,f(x)取得最大值为
,当x=3时,f(x)取得最小值为-2.
再根据f(x)为奇函数,f(0)=0,可得f(x)=
|
(2)当x∈[1,3]时,由于二次函数f(x)在[1,
| 3 |
| 2 |
| 3 |
| 2 |
故当x=
| 3 |
| 2 |
| 1 |
| 4 |
点评:本题主要考查利用函数的奇偶性求函数的解析式,求二次函数在闭区间上的最值,属于基础题.

练习册系列答案
相关题目
已知点A(-1,2),B(2,-2),C(0,3),若点M(a,b)(a≠0)是线段AB上一点,则直线CM的斜率的取值范围是( )
A、(-∞,-
| ||
| B、[1,+∞] | ||
C、(-∞,-
| ||
D、[-
|
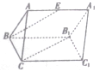 三棱柱ABC-A1B1C1的各棱相等,AA1⊥底面ABC,E是AA1的中点.
三棱柱ABC-A1B1C1的各棱相等,AA1⊥底面ABC,E是AA1的中点.