题目内容
连续抛掷两枚正方体骰子(它们的六个面分别标有1,2,3,4,5,6),记所得朝上的面的点数分别为x,y,过坐标原点和点P(x,y)的直线的倾斜角为θ,则θ>60°的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:列举法计算基本事件数及事件发生的概率
专题:概率与统计
分析:求出过坐标原点和点P(x,y)的直线的倾斜角为θ>60的等价条件,利用古典概型的概率公式即可得到结论.
解答:
解:过坐标原点和点P(x,y)的直线的倾斜角为θ,则θ>60°,即tan°θ>
,
即
>
,即y>
x
若x=1,则y>
,此时y=2,3,4,5,6,
若x=2,则y>2
,此时y=4,5,6,
若x=3,则y>3
,此时y=6,
若x=4,则y>4
,此时y不存在
若x=5,则y>5
,此时y不存在,共有9种,
过坐标原点和点P(x,y)的直线的倾斜角为θ,则θ>60°的概率为
=
,
故选:A
| 3 |
即
| y |
| x |
| 3 |
| 3 |
若x=1,则y>
| 3 |
若x=2,则y>2
| 3 |
若x=3,则y>3
| 3 |
若x=4,则y>4
| 3 |
若x=5,则y>5
| 3 |
过坐标原点和点P(x,y)的直线的倾斜角为θ,则θ>60°的概率为
| 9 |
| 36 |
| 1 |
| 4 |
故选:A
点评:本题主要考查概率的计算,利用数量积求出过坐标原点和点P(x,y)的直线的倾斜角为θ>60的等价条件是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
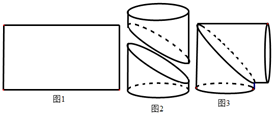 工人师傅在如图1的一块矩形铁皮上画一条曲线,沿曲线剪开,将所得到的两部分卷成圆柱状,如图2,然后将其对接,可做成一个直角的“拐脖”,如图3.工人师傅所画的曲线是( )
工人师傅在如图1的一块矩形铁皮上画一条曲线,沿曲线剪开,将所得到的两部分卷成圆柱状,如图2,然后将其对接,可做成一个直角的“拐脖”,如图3.工人师傅所画的曲线是( )| A、一段圆弧 |
| B、一段抛物线 |
| C、一段双曲线 |
| D、一段正弦曲线 |
已知△ABC中,点D在BC边上,且
=4
=r
+s
,则3r+s=( )
| CD |
| DB |
| AB |
| AC |
A、
| ||
B、
| ||
C、
| ||
D、
|
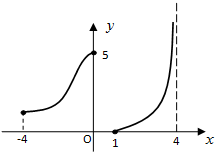 如图所示是函数y=f(x)的图象,图中曲线与直线无限接近但是永不相交,则以下描述正确的是( )
如图所示是函数y=f(x)的图象,图中曲线与直线无限接近但是永不相交,则以下描述正确的是( )| A、函数f(x)的定义域为[-4,4) |
| B、函数f(x)的值域为[0,5] |
| C、此函数在定义域中不单调 |
| D、对于任意的y∈[0,+∞),都有唯一的自变量x与之对应 |
若关于x,y的方程x2•sinα-y2•cosα=1所表示的焦点在x轴的双曲线,则方程(x+cosα)2+(y+sinα)2=1所表示的圆的圆心在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
在△ABC中,A,B,C所对的边分别是a,b,c,满足3a2+3b2=c2+4ab,现设f(x)=tanx,则( )
| A、f(sinA)≤f(cosB) |
| B、f(sinA)≥f(cosB) |
| C、f(sinA)≤f(sinB) |
| D、f(cosA)≤f(cosB) |
已知A={x|
>1},B={x||x|<a},若∅?B⊆A,则实数a的取值范围是( )
| 4 |
| x+1 |
| A、a<1 | B、a≤1 |
| C、1≤a≤3 | D、0<a≤1 |