题目内容
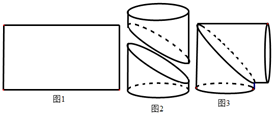工人师傅在如图1的一块矩形铁皮上画一条曲线，沿曲线剪开，将所得到的两部分卷成圆柱状，如图2，然后将其对接，可做成一个直角的“拐脖”，如图3．工人师傅所画的曲线是（ ）| A、一段圆弧 |
| B、一段抛物线 |
| C、一段双曲线 |
| D、一段正弦曲线 |
考点：平面与圆柱面的截线
专题：选作题,矩阵和变换
分析：利用平面图分析曲线的对称性，即可得出结论．
解答：
解：将图2剪开展成平面图分析可知，曲线为轴对称图形，将图3剪开展成平面图分析可知，曲线也为中心对称图形．所以此曲线即为轴对称图形又为中心对称图形，故只有D正确．
故选：D．
故选：D．
点评：本题考查平面与圆柱面的截线，考查函数的对称性和奇偶性，比较基础．
练习册系列答案
相关题目
函数f（x）=lnx+x3-9的零点所在的区间为（ ）
| A、（0，1） |
| B、（1，2） |
| C、（2，3） |
| D、（3，4） |
已如f（x）是定义在R上的偶函数，且满足f（x+2）=f（x），当x∈[0，1]时，f（x）=2x．若在区间[-2，3]上方程ax+2a-f（x）=0恰有四个不相等的实数根，则实数a的取值范围 是（ ）
A、(
| ||||
B、(
| ||||
C、(0，
| ||||
D、(0，
|
已知函数f（x）=x2-2ax+6在区间（-∞，3）是减函数，则（ ）
| A、a≥3 | B、a＞0 |
| C、a≤3 | D、a＜3 |
若
与
不共线，实数x、y满足等式2x
+（3-y）
=x
+（3y+1）
，则实数x+y=（ ）
| a |
| b |
| a |
| b |
| b |
| a |
| A、1 | B、2 | C、3 | D、-2 |
设点P是以F1，F2为左、右焦点的双曲线
-
=1（a＞0，b＞0）左支上一点，且满足
•
=0，tan∠PF2F1=
，则此双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| PF1 |
| PF2 |
| 2 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|