题目内容
若关于x，y的方程x2•sinα-y2•cosα=1所表示的焦点在x轴的双曲线，则方程（x+cosα）2+（y+sinα）2=1所表示的圆的圆心在（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
考点：双曲线的简单性质
专题：计算题,直线与圆
分析：由于方程x2•sinα-y2•cosα=1所表示的焦点在x轴的双曲线，结合三角函数的符号可得sinα＞0，cosα＞0，而圆（x+cosα）2+（y+sinα）2=1的圆心坐标为（-cosα，-sinα），根据其坐标的特点即可得出结论．
解答：
解：∵方程x2•sinα-y2•cosα=1所表示的焦点在x轴的双曲线，
∴sinα＞0，cosα＞0，
而圆（x+cosα）2+（y+sinα）2=1的圆心坐标为（-cosα，-sinα）
结合三角函数的符号可得，圆心的横坐标与纵坐标均为负，
故其位置在第三象限．
故选：C．
∴sinα＞0，cosα＞0，
而圆（x+cosα）2+（y+sinα）2=1的圆心坐标为（-cosα，-sinα）
结合三角函数的符号可得，圆心的横坐标与纵坐标均为负，
故其位置在第三象限．
故选：C．
点评：本题考查双曲线的简单性质，双曲线的标准方程的特征，结合三角函数的符号性可得sinα＞0，cosα＞0是解题的关键．
练习册系列答案
通城学典默写能手系列答案
相关题目
若
与
不共线，实数x、y满足等式2x
+（3-y）
=x
+（3y+1）
，则实数x+y=（ ）
| a |
| b |
| a |
| b |
| b |
| a |
| A、1 | B、2 | C、3 | D、-2 |
执行如图所示的程序框图，若输出的k=6，则输入的整数p的最大值为（ ）
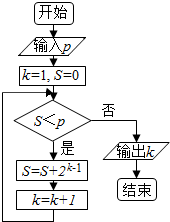
| A、7 | B、15 | C、31 | D、63 |
连续抛掷两枚正方体骰子（它们的六个面分别标有1，2，3，4，5，6），记所得朝上的面的点数分别为x，y，过坐标原点和点P（x，y）的直线的倾斜角为θ，则θ＞60°的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
长方体的一个顶点上三条棱长分别是1、2、3，且它的8个顶点都在同一球面上，则这个球的表面积是（ ）
| A、7π | B、14π |
| C、28π | D、56π |
点（a，b）在直线2x-y+3=0的右下方，则（ ）
| A、2a-b+3＜0 |
| B、2a-b+3＞0 |
| C、2a-b+3=0 |
| D、以上都不成立 |
如图，已知鞭形ABEF所在平面与直角梯形ABCD所在平面互相垂直，AB=2AD=2CD=4，∠BAD=∠CDA=90°，∠EFA=60°，点H，G分别是线段EF，BC的中点，点M为HE的中点．