题目内容
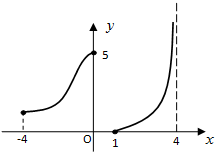 如图所示是函数y=f(x)的图象,图中曲线与直线无限接近但是永不相交,则以下描述正确的是( )
如图所示是函数y=f(x)的图象,图中曲线与直线无限接近但是永不相交,则以下描述正确的是( )| A、函数f(x)的定义域为[-4,4) |
| B、函数f(x)的值域为[0,5] |
| C、此函数在定义域中不单调 |
| D、对于任意的y∈[0,+∞),都有唯一的自变量x与之对应 |
考点:函数的图象
专题:函数的性质及应用
分析:通过函数的定义域判断A的正误;函数的值域判断B、C的正误;利用公式的单调性判断D的正误;
解答:
解:由已知条件以及函数的图象可知,函数的定义域为[-4,0]∪[1,4),所以A不正确;
函数的值域为:[0,+∞),所以B不正确;
函数在[-4,0],[1,4)是增函数,这个定义域上不是增函数,所以C正确.
由函数的图象,可知D不正确;
故选:C.
函数的值域为:[0,+∞),所以B不正确;
函数在[-4,0],[1,4)是增函数,这个定义域上不是增函数,所以C正确.
由函数的图象,可知D不正确;
故选:C.
点评:本题考查函数的基本性质:定义域、值域以及单调性的判断与应用.

练习册系列答案
 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
已知函数f(x)=x2-2ax+6在区间(-∞,3)是减函数,则( )
| A、a≥3 | B、a>0 |
| C、a≤3 | D、a<3 |
设点P是以F1,F2为左、右焦点的双曲线
-
=1(a>0,b>0)左支上一点,且满足
•
=0,tan∠PF2F1=
,则此双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| PF1 |
| PF2 |
| 2 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
读程序框图,则循环体执行的次数( ),程序输出结果是( )


| A、49,2045 |
| B、50,2540 |
| C、50,2450 |
| D、49,2450 |
连续抛掷两枚正方体骰子(它们的六个面分别标有1,2,3,4,5,6),记所得朝上的面的点数分别为x,y,过坐标原点和点P(x,y)的直线的倾斜角为θ,则θ>60°的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
(2x-1)4(2x+1)6的展开式中含x4的系数为( )
| A、-32 | B、32 |
| C、-92 | D、100 |
已知二次函数f(x)的图象是一条开口向下的抛物线,且对任意x∈R,均有f(1-x)=f(1+x) 成立.下列不等式中正确的是( )
A、f(
| ||||
| B、f(-1)>f(2) | ||||
| C、f(-1)<f(2) | ||||
| D、f(0)<0 |
 如图,酒杯的形状为倒立的圆锥,杯深8cm,上口宽6cm,水以20cm2/s的流量倒入杯中,当水深为4cm时,求水面升高的瞬时变化率.
如图,酒杯的形状为倒立的圆锥,杯深8cm,上口宽6cm,水以20cm2/s的流量倒入杯中,当水深为4cm时,求水面升高的瞬时变化率.