题目内容
9.设Sn为数列{an}的前n项和,且a3-a1=3,$\frac{{S}_{n+1}-1}{{S}_{n}}$=$\frac{{a}_{2}}{{a}_{1}}$=p(p>0,n∈N*)(1)求数列{an}的通项公式;
(2)求数列{an+(-1)nlog2an}的前2n项和.
分析 (1)令n=1时,求得a1=1,a3=4,可得Sn+1=2Sn+1,再把n换为n-1,两式相减,结合等比数列的通项公式,即可得到所求;
(2)求得an+(-1)nlog2an=2n-1+(-1)n•(n-1),再由数列的求和方法:分组求和,可得所求和.
解答 解:(1)由题意可得$\frac{{S}_{2}-1}{{S}_{1}}$=$\frac{{a}_{2}}{{a}_{1}}$,
即有a1+a2-1=a2,可得a1=1,a3=4,
又$\frac{{S}_{3}-1}{{S}_{2}}$=$\frac{{a}_{2}}{{a}_{1}}$,即为1+a2+4-1=a2(1+a2),
解得a2=2,(负的舍去),
则$\frac{{S}_{n+1}-1}{{S}_{n}}$=$\frac{{a}_{2}}{{a}_{1}}$=p=2,即Sn+1=2Sn+1,
可得Sn=2Sn-1+1,
两式相减可得,an+1=2an,
则有an=2•2n-2=2n-1,对n=1也成立,
故an=2n-1(n∈N*);
(2)an+(-1)nlog2an=2n-1+(-1)n•(n-1),
前2n项和为S2n=$\frac{1-{2}^{2n}}{1-2}$+(0+1)+(-2+3)+…+(2-2n+2n-1)
=22n+n-1.
点评 本题考查数列的通项的求法,注意运用n>1时,an=Sn-Sn-1,以及等比数列的通项公式,考查数列的求和方法:分组求和,考查运算能力,属于中档题.

练习册系列答案
相关题目
14.“tana=2”是“tan2a=-$\frac{4}{3}$”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
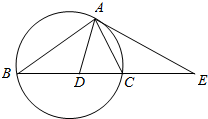 如图,△ABC的外接圆的切线AE与BC的延长线相交于点E,∠BAC的平分线与BC相交于点D,求证:
如图,△ABC的外接圆的切线AE与BC的延长线相交于点E,∠BAC的平分线与BC相交于点D,求证: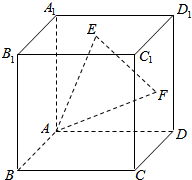 如图,在正方体ABCD-A1B1C1D1中,E、F分别为A1B1C1D1,CDD1C1的中心,试用向量$\overrightarrow{{B}_{1}B}$,$\overrightarrow{{B}_{1}{C}_{1}}$,$\overrightarrow{{B}_{1}{A}_{1}}$表示向量:
如图,在正方体ABCD-A1B1C1D1中,E、F分别为A1B1C1D1,CDD1C1的中心,试用向量$\overrightarrow{{B}_{1}B}$,$\overrightarrow{{B}_{1}{C}_{1}}$,$\overrightarrow{{B}_{1}{A}_{1}}$表示向量: