题目内容
19．
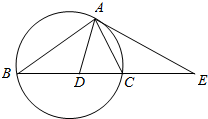如图，△ABC的外接圆的切线AE与BC的延长线相交于点E，∠BAC的平分线与BC相交于点D，求证：（1）EA=ED；
（2）DB•DE=DC•BE．
分析 （1）利用圆的切线以及角的平分线，证明三角形是等腰三角形，推出结果．
（2）通过证明△ABE∽△CAE，结合（1）然后证明DB•DE=DC•BE．
解答 证明：（1）∵∠ADE=∠ABD+∠BAD，∠DAE=∠DAC+∠EAC，
而∠ABD=∠EAC，∠BAD=∠DAC，∴∠ADE=∠DAE，
三角形ADE是等腰三角形．
∴EA=ED．…（5分）
（2）∵$\left\{\begin{array}{l}∠ABE=∠CAE，\;\;\\∠AEB=∠CEA，\;\;\end{array}\right.$∴△ABE∽△CAE，
∵∠ABE=∠CAE，∴$\frac{AB}{AC}=\frac{BE}{AE}$，
又∵$\frac{AB}{AC}=\frac{DB}{DC}$，∴$\frac{DB}{DC}=\frac{BE}{AE}$，即DB•AE=DC•BE，
由（Ⅰ）知EA=ED，∴DB•DE=DC•BE．…（10分）
点评 本题考查圆的内接多边形，三角形相似以及弦切角的知识的应用，考查推理与证明．
练习册系列答案
相关题目
4．设函数f（x）是奇函数，并且在R上为增函数，若0≤θ≤$\frac{π}{6}$时，f（msinθ）+f（1-m）＞0恒成立，则实数m的取值范围是（ ）
| A． | （0，1） | B． | （0，$\frac{1}{2}$） | C． | （-∞，2） | D． | （-∞，1） |