题目内容
数列{an}满足an>0(n∈N*),Sn为数列{an}前n项和,并且满足Sn=
(an+
).求
(1)S1,S2,S3的值;
(2)猜想Sn的表达式,并用数学归纳法证明.
| 1 |
| 2 |
| 1 |
| an |
(1)S1,S2,S3的值;
(2)猜想Sn的表达式,并用数学归纳法证明.
考点:数学归纳法
专题:点列、递归数列与数学归纳法
分析:(1)由题设条件,分别令n=1,2,3,能够求出a1,a2,a3.即可求得S1,S2,S3的值.
(2)由(1)猜想数列{an}的通项公式:Sn=
,(n∈N*),检验n=1时等式成立,假设n=k时命题成立,证明当n=k+1时命题也成立.
(2)由(1)猜想数列{an}的通项公式:Sn=
| n |
解答:
解:(1)易求得a1=1,a2=
-1,a3=
-
,
S1=1,S2=
,S3=
(3分);
(2)猜想Sn=
(5分)
证明:Sn=
(an+
).Sn-1=
(an-1+
).可得an=
-
,
①当n=1时,a1=
=1,猜想成立
②假设n=k时,Sk=
成立,(8分)
则n=k+1时,Sk+1=Sk+ak+1=
+ak+1=
+
-
=
.
即n=k+1时,猜想也成立.
由①②知,n∈N*时,Sn=
.(12分)
| 2 |
| 3 |
| 2 |
S1=1,S2=
| 2 |
| 3 |
(2)猜想Sn=
| n |
证明:Sn=
| 1 |
| 2 |
| 1 |
| an |
| 1 |
| 2 |
| 1 |
| an-1 |
| n |
| n-1 |
①当n=1时,a1=
| 1 |
②假设n=k时,Sk=
| k |
则n=k+1时,Sk+1=Sk+ak+1=
| k |
| k |
| k+1 |
| k |
| k+1 |
即n=k+1时,猜想也成立.
由①②知,n∈N*时,Sn=
| n |
点评:本题是中档题,考查数列递推关系式的应用,数学归纳法证明数列问题的方法,考查逻辑推理能力,计算能力.注意在证明n=k+1时用上假设,化为n=k的形式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
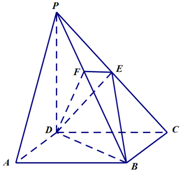 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PDC⊥底面ABCD,PD=DC,∠PDC=90°,E是PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PDC⊥底面ABCD,PD=DC,∠PDC=90°,E是PC的中点.