题目内容
若函数f(x)=asinx+bcosx(a,b∈R),非零向量
=(a,b),我们称
为函数f(x)的“相伴向量”,f(x)为向量
的“相伴函数”.
(Ⅰ)已知函数f(x)=(sinωx+cosωx)2+2cos2ωx-2(ω>0)的最小正周期为2π,求函数f(x)的“相伴向量”;
(Ⅱ)记向量
=(
,1)的“相伴函数”为g(x),将g(x)图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得的图象上所有点向左平移
个单位长度,得到函数h(x),若h(2α+
)=
,α∈(0,
),求sinα的值;
(Ⅲ)对于函数φ(x)=sinxcos2x,是否存在“相伴向量”?若存在,求出φ(x)“相伴向量”;若不存在,请说明理由.
| m |
| m |
| m |
(Ⅰ)已知函数f(x)=(sinωx+cosωx)2+2cos2ωx-2(ω>0)的最小正周期为2π,求函数f(x)的“相伴向量”;
(Ⅱ)记向量
| n |
| 3 |
| 2π |
| 3 |
| π |
| 3 |
| 6 |
| 5 |
| π |
| 2 |
(Ⅲ)对于函数φ(x)=sinxcos2x,是否存在“相伴向量”?若存在,求出φ(x)“相伴向量”;若不存在,请说明理由.
考点:平面向量数量积的运算,三角函数的周期性及其求法
专题:三角函数的图像与性质,平面向量及应用
分析:(I)利用三角函数基本关系式、倍角公式、两角和差的正弦公式、三角函数的性质、“相伴向量”的定义即可得出;
(II)利用“相伴函数”的定义可得:g(x)=
sinx+cosx=2sin(x+
),再利用三角函数的变换法则可得h(x)=2sin[
(x+
)+
],化为h(x)=2cos
x.
由于h(2α+
)=
,可得cos(α+
)=
,利用α∈(0,
),可得α+
∈(
,
),进而得到sin(α+
)=
,再利用sinα=sin[(α+
)-
]展开即可得出.
(III)若函数φ(x)=sinxcos2x存在“相伴向量”,则存在a,b,使得sinxcos2x=asinx+bcosx对任意的x∈R都成立,通过对x取值即可判断出.
(II)利用“相伴函数”的定义可得:g(x)=
| 3 |
| π |
| 6 |
| 1 |
| 2 |
| 2π |
| 3 |
| π |
| 6 |
| 1 |
| 2 |
由于h(2α+
| π |
| 3 |
| 6 |
| 5 |
| π |
| 6 |
| 3 |
| 5 |
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| 2π |
| 3 |
| π |
| 6 |
| 4 |
| 5 |
| π |
| 6 |
| π |
| 6 |
(III)若函数φ(x)=sinxcos2x存在“相伴向量”,则存在a,b,使得sinxcos2x=asinx+bcosx对任意的x∈R都成立,通过对x取值即可判断出.
解答:
解:(Ⅰ)f(x)=(sinωx+cosωx)2+2cos2ωx-2=sin2ωx+cos2ωx+sin2ωx+1+cos2ωx-2=sin2ωx+cos2ωx=
sin(2ωx+
),
依题意得
=2π,故ω=
.
∴f(x)=sinx+cosx,即f(x)的“相伴向量”为(1,1).
(Ⅱ)依题意,g(x)=
sinx+cosx=2sin(x+
),
将g(x)图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),
得到函数y=2sin(
x+
),
再将所得的图象上所有点向左平移
个单位长度,得到h(x)=2sin[
(x+
)+
],即h(x)=2sin(
x+
)=2cos
x,
∵h(2α+
)=
,∴cos(α+
)=
,
∵α∈(0,
),∴α+
∈(
,
),∴sin(α+
)=
,
∴sinα=sin[(α+
)-
]=sin(α+
)cos
-cos(α+
)sin
=
.
(Ⅲ)若函数φ(x)=sinxcos2x存在“相伴向量”,
则存在a,b,使得sinxcos2x=asinx+bcosx对任意的x∈R都成立,
令x=0,得b=0,
因此sinxcos2x=asinx,即sinx=0或cos2x=a,
显然上式对任意的x∈R不都成立,
∴函数φ(x)=sinxcos2x不存在“相伴向量”.
| 2 |
| π |
| 4 |
依题意得
| 2π |
| 2ω |
| 1 |
| 2 |
∴f(x)=sinx+cosx,即f(x)的“相伴向量”为(1,1).
(Ⅱ)依题意,g(x)=
| 3 |
| π |
| 6 |
将g(x)图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),
得到函数y=2sin(
| 1 |
| 2 |
| π |
| 6 |
再将所得的图象上所有点向左平移
| 2π |
| 3 |
| 1 |
| 2 |
| 2π |
| 3 |
| π |
| 6 |
| 1 |
| 2 |
| π |
| 2 |
| 1 |
| 2 |
∵h(2α+
| π |
| 3 |
| 6 |
| 5 |
| π |
| 6 |
| 3 |
| 5 |
∵α∈(0,
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| 2π |
| 3 |
| π |
| 6 |
| 4 |
| 5 |
∴sinα=sin[(α+
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
4
| ||
| 10 |
(Ⅲ)若函数φ(x)=sinxcos2x存在“相伴向量”,
则存在a,b,使得sinxcos2x=asinx+bcosx对任意的x∈R都成立,
令x=0,得b=0,
因此sinxcos2x=asinx,即sinx=0或cos2x=a,
显然上式对任意的x∈R不都成立,
∴函数φ(x)=sinxcos2x不存在“相伴向量”.
点评:本题考查了三角函数基本关系式、倍角公式、两角和差的正弦公式、三角函数的性质、“相伴向量”的定义、“相伴函数”的定义、三角函数的变换方法、同角三角函数基本关系式、两角和差的正弦公式等基础知识与基本技能方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
相关题目
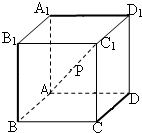 在正方体AC1中,若点P在对角线AC1上,且P点到三条棱CD、A1D1、BB1的距离都相等,则这样的点共有( )
在正方体AC1中,若点P在对角线AC1上,且P点到三条棱CD、A1D1、BB1的距离都相等,则这样的点共有( )| A、1个 | B、2个 |
| C、3个 | D、无穷多个 |
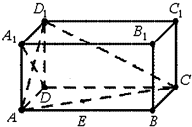 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2.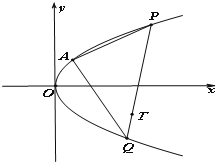 如图,已知过点A(1,2)的抛物线C:y2=ax与过点T(3,-2)的动直线l相交于P、Q两点.
如图,已知过点A(1,2)的抛物线C:y2=ax与过点T(3,-2)的动直线l相交于P、Q两点.