题目内容
已知数列{an},定义其平均数是Vn=
,n∈N*.
(Ⅰ)若数列{an}的平均数Vn=2n+1,求an;
(Ⅱ)若数列{an}是首项为1,公比为2的等比数列,其平均数为Vn,求证:
+
+…+
<4.(提示
<
)
| a1+a2+…+an |
| n |
(Ⅰ)若数列{an}的平均数Vn=2n+1,求an;
(Ⅱ)若数列{an}是首项为1,公比为2的等比数列,其平均数为Vn,求证:
| 1 |
| V1 |
| 1 |
| V2 |
| 1 |
| Vn |
| n |
| 2n-1 |
| n |
| 2n-1 |
考点:基本不等式,等比数列的性质
专题:新定义,等差数列与等比数列
分析:(Ⅰ)由Vn=
,得
=2n+1,变形得a1+a2+…+an=2n2+n,据此可求an;
(Ⅱ)由等比数列的前n项和公式及平均数的定义可得Vn=
,从而得
=
<
,于是
+
+…+
<1+
+
+…+
,令Sn=1+
+
+…+
,利用错位相减法可求得Sn,进而可得结论;
| a1+a2+…+an |
| n |
| a1+a2+…+an |
| n |
(Ⅱ)由等比数列的前n项和公式及平均数的定义可得Vn=
| 2n-1 |
| n |
| 1 |
| Vn |
| n |
| 2n-1 |
| n |
| 2n-1 |
| 1 |
| V1 |
| 1 |
| V2 |
| 1 |
| Vn |
| 2 |
| 2 |
| 3 |
| 22 |
| n |
| 2n-1 |
| 2 |
| 2 |
| 3 |
| 22 |
| n |
| 2n-1 |
解答:
解:(Ⅰ)因为Vn=
,
所以
=2n+1.
变形得 a1+a2+…+an=2n2+n,①
当n≥2时有 a1+a2+…+an-1=2(n-1)2+(n-1)②,
①-②得an=4n-1(n≥2).
又当n=1时,V1=a1=2×1+1=3,
适合an=4n-1.
故an=4n-1(n∈N*).
(Ⅱ)数列{an}的前n项和:a1+a2+…+an=
=2n-1,
∴Vn=
,
=
<
,
∴
+
+…+
<1+
+
+…+
,
令Sn=1+
+
+…+
①,则
Sn=
+
+
+…+
②,
①-②,得
Sn=1+
+
+…+
-
=
-
=2[1-(
)n]-
,
∴Sn=4-
,
∴
+
+…+
<4-
<4.
| a1+a2+…+an |
| n |
所以
| a1+a2+…+an |
| n |
变形得 a1+a2+…+an=2n2+n,①
当n≥2时有 a1+a2+…+an-1=2(n-1)2+(n-1)②,
①-②得an=4n-1(n≥2).
又当n=1时,V1=a1=2×1+1=3,
适合an=4n-1.
故an=4n-1(n∈N*).
(Ⅱ)数列{an}的前n项和:a1+a2+…+an=
| 1-2n |
| 1-2 |
∴Vn=
| 2n-1 |
| n |
| 1 |
| Vn |
| n |
| 2n-1 |
| n |
| 2n-1 |
∴
| 1 |
| V1 |
| 1 |
| V2 |
| 1 |
| Vn |
| 2 |
| 2 |
| 3 |
| 22 |
| n |
| 2n-1 |
令Sn=1+
| 2 |
| 2 |
| 3 |
| 22 |
| n |
| 2n-1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 22 |
| 3 |
| 23 |
| n |
| 2n |
①-②,得
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n-1 |
| n |
| 2n |
1-(
| ||
1-
|
| n |
| 2n |
| 1 |
| 2 |
| n |
| 2n |
∴Sn=4-
| 2+n |
| 2n-1 |
∴
| 1 |
| V1 |
| 1 |
| V2 |
| 1 |
| Vn |
| 2+n |
| 2n-1 |
点评:本题考查数列的通项公式的求法,考查数列的前n项和公式的应用.解题时要认真审题,仔细解答,注意等价转化思想的合理运用.

练习册系列答案
相关题目
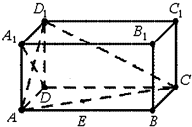 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2.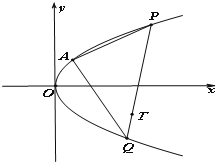 如图,已知过点A(1,2)的抛物线C:y2=ax与过点T(3,-2)的动直线l相交于P、Q两点.
如图,已知过点A(1,2)的抛物线C:y2=ax与过点T(3,-2)的动直线l相交于P、Q两点.