题目内容
已知二次函数f(x)=ax2+4ax+a2-1
(1)当a<0时,求函数f(x)的单调区间
(2)当x∈[-4,1]时,函数f(x)的最大值为5,求实数a的值.
(1)当a<0时,求函数f(x)的单调区间
(2)当x∈[-4,1]时,函数f(x)的最大值为5,求实数a的值.
考点:二次函数的性质
专题:函数的性质及应用
分析:(1)根据对称轴方程以及a的符号,求得函数的单调区间.
(2)根据对称轴为x=-2∈[-4,1],分当a>0和当a<0两种情况,分别根据函数的最大值求得a的值.
(2)根据对称轴为x=-2∈[-4,1],分当a>0和当a<0两种情况,分别根据函数的最大值求得a的值.
解答:
解:(1)∵对称轴为x=-2,∴当a<0时,函数f(x)在(-∞,-2]上是增函数,
在[-2,+∞)上是减函数.
(2)∵对称轴为x=-2∈[-4,1],
①当a>0时,fmax(x)=f(1)=a2+5a-1=5,∴a=1,或a=-6(舍去).
②当a<0时,fmax(x)=f(-2)=a2-4a-1=5,∴a=2-
或a=2+
(舍去).
综上所述,a=1或a=2-
.
在[-2,+∞)上是减函数.
(2)∵对称轴为x=-2∈[-4,1],
①当a>0时,fmax(x)=f(1)=a2+5a-1=5,∴a=1,或a=-6(舍去).
②当a<0时,fmax(x)=f(-2)=a2-4a-1=5,∴a=2-
| 10 |
| 10 |
综上所述,a=1或a=2-
| 10 |
点评:本题主要考查二次函数的性质应用,体现了分类讨论的数学思想,属于基础题.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案
相关题目
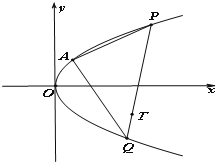 如图,已知过点A(1,2)的抛物线C:y2=ax与过点T(3,-2)的动直线l相交于P、Q两点.
如图,已知过点A(1,2)的抛物线C:y2=ax与过点T(3,-2)的动直线l相交于P、Q两点. 如图,在△ABC中,∠BAC=120°,AB=2,AC=1.D是BC边上的一点(不含端点),则
如图,在△ABC中,∠BAC=120°,AB=2,AC=1.D是BC边上的一点(不含端点),则