题目内容
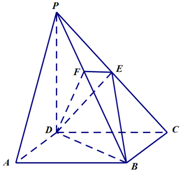 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PDC⊥底面ABCD,PD=DC,∠PDC=90°,E是PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PDC⊥底面ABCD,PD=DC,∠PDC=90°,E是PC的中点.(Ⅰ)求证:PA∥平面EDB;
(Ⅱ)若EF⊥PB于F,求证:PB⊥平面EFD;
(Ⅲ)若DC=2,求三棱锥E-BCD的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定,直线与平面垂直的判定
专题:综合题,空间位置关系与距离
分析:(Ⅰ)由线面平行的判定定理,须先作辅助线证线线平行,从而可证线面平行;
(Ⅱ)由线面垂直的判定定理,须先证PB垂直于平面内的两条相交直线,从而可证线面垂直;
(Ⅲ)取DC中点G,连接EG,证明EG⊥平面ABCD,利用VE-BCD=
S△BCD•EG,即可求出三棱锥E-BCD的体积.
(Ⅱ)由线面垂直的判定定理,须先证PB垂直于平面内的两条相交直线,从而可证线面垂直;
(Ⅲ)取DC中点G,连接EG,证明EG⊥平面ABCD,利用VE-BCD=
| 1 |
| 3 |
解答:
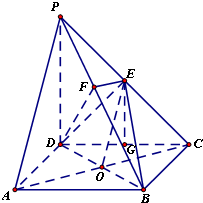 (I)证明:在正方形ABCD中,连接AC,交BD于O点,连接EO,
(I)证明:在正方形ABCD中,连接AC,交BD于O点,连接EO,
∵四边形ABCD为正方形,∴O为AC中点,
∵E为PC中点,∴EO∥PA,
∵PA?面EDB,EO?面EDB,
∴:PA∥平面EDB;
(II)证明:∵侧面PDC⊥底面ABCD,且侧面PDC∩底面ABCD=CD,
在面ABCD中,BC⊥CD,
∴BC⊥面PCD
∴BC⊥DE
又∵PD=DC,E是PC的中点
∴PC⊥DE
又∵PC∩BC=C
∴DE⊥面PBC
∴DE⊥PB
又∵EF⊥PB,DE∩EF=E
∴PB⊥平面EFD.
(III)解:取DC中点G,连接EG.∴EG∥PD,EG=1,
∵PD⊥DC,侧面PDC⊥底面ABCD,且侧面PDC∩底面ABCD=CD,
∴PD⊥平面ABCD,∴EG⊥平面ABCD,
∴VE-BCD=
S△BCD•EG=
(
BC•DC)•EG=
.
 (I)证明:在正方形ABCD中,连接AC,交BD于O点,连接EO,
(I)证明:在正方形ABCD中,连接AC,交BD于O点,连接EO,∵四边形ABCD为正方形,∴O为AC中点,
∵E为PC中点,∴EO∥PA,
∵PA?面EDB,EO?面EDB,
∴:PA∥平面EDB;
(II)证明:∵侧面PDC⊥底面ABCD,且侧面PDC∩底面ABCD=CD,
在面ABCD中,BC⊥CD,
∴BC⊥面PCD
∴BC⊥DE
又∵PD=DC,E是PC的中点
∴PC⊥DE
又∵PC∩BC=C
∴DE⊥面PBC
∴DE⊥PB
又∵EF⊥PB,DE∩EF=E
∴PB⊥平面EFD.
(III)解:取DC中点G,连接EG.∴EG∥PD,EG=1,
∵PD⊥DC,侧面PDC⊥底面ABCD,且侧面PDC∩底面ABCD=CD,
∴PD⊥平面ABCD,∴EG⊥平面ABCD,
∴VE-BCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
点评:本题考查线面平行的判定定理、线面垂直的判定定理和性质定理,考查三棱锥体积的计算,须能灵活应用这些定理,并有较强的空间立体感.属中等题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
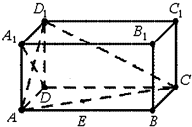 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2.