题目内容
如图，AB、CD分别与半圆O切于点A、D，BC切半圆O于点E，若AB=4，CD=9，求⊙O的半径．
考点：与圆有关的比例线段
专题：立体几何
分析：从B点做CD垂线交CD于F，则ABFD是矩形，因为BE=BA=4，CD=CE=9，所以BC=13，由此能求出⊙O的半径．
解答：
解：如图所示：
从B点做CD垂线交CD于F，则ABFD是矩形，
因为BE=BA=4，CD=CE=9，所以BC=13，
在直角三角形BCF中，BC=13，CF=9-4=5，则BF=12，
所以半圆的直径AD=BF=12，
∴⊙O的半径为r=6．
从B点做CD垂线交CD于F，则ABFD是矩形，
因为BE=BA=4，CD=CE=9，所以BC=13，
在直角三角形BCF中，BC=13，CF=9-4=5，则BF=12，
所以半圆的直径AD=BF=12，
∴⊙O的半径为r=6．
点评：本题考查圆的半径的求法，是基础题，解题时要认真审题，注意圆的性质的合理运用．
练习册系列答案
阅读快车系列答案
相关题目
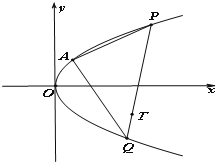如图，已知过点A（1，2）的抛物线C：y2=ax与过点T（3，-2）的动直线l相交于P、Q两点．
如图，在△ABC中，∠BAC=120°，AB=2，AC=1．D是BC边上的一点（不含端点），则