题目内容
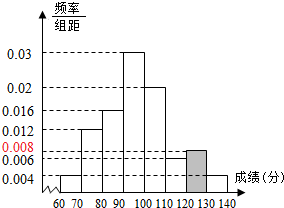
 某校在一次期末数学统测中,为统计学生的考试情况,从学校的2000名学生中随机抽取50名学生的考试成绩,被测学生成绩全部介于60分到140分之间(满分150分),将统计结果按如下方式分成八组:第一组[60,70),第二组[70,80),…,第八组[130,140],如图是按上述分组方法得到的频率分布直方图的一部分.
某校在一次期末数学统测中,为统计学生的考试情况,从学校的2000名学生中随机抽取50名学生的考试成绩,被测学生成绩全部介于60分到140分之间(满分150分),将统计结果按如下方式分成八组:第一组[60,70),第二组[70,80),…,第八组[130,140],如图是按上述分组方法得到的频率分布直方图的一部分. (Ⅰ)求第七组的频率,并完成频率分布直方图;
(Ⅱ)估计该校的2000名学生这次考试成绩的平均分(可用中值代替各组数据平均值);
(Ⅲ)若从样本成绩属于第六组和第八组的所有学生中随机抽取两名,求他们的分差不小于10分的概率.
考点:古典概型及其概率计算公式,频率分布直方图,众数、中位数、平均数
专题:概率与统计
分析:(Ⅰ)根据所有频率之和等于1求出第七组的频率,然后绘图即可;
(Ⅱ)利用平均数计算公式计算即可;
(Ⅲ)一一列举所有满足从中任取2人的所有基本事件,找到分差在(10分)以上的基本事件,利用概率公式计算即可.
(Ⅱ)利用平均数计算公式计算即可;
(Ⅲ)一一列举所有满足从中任取2人的所有基本事件,找到分差在(10分)以上的基本事件,利用概率公式计算即可.
解答:
解:(Ⅰ)由频率分布直方图知第七组频率为:f7=1-(0.004+0.012+0.016+0.03+0.02+0.006+0.004)×10=0.08;
直方图如图所示.
(Ⅱ)该校这次考试的平均成绩为:65×0.04+75×0.12+85×0.16+95×0.3+105×0.2+115×0.06+125×0.08+135×0.04=97,
(Ⅲ)第六组有学生3人,分别记作A1,A2,A3,第八组有学生2人,分别记作B1,B2;
则从中任取2人的所有基本事件为 (A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(A1,A2),(A1,A3),A2,A3),(B1,B2)共10个.
分差在(10分)以上,表示所选2人来自不同组,其基本事件有6个:(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),
所以从中任意抽取2人,分差在(10分)以上的概率P=
=
.
直方图如图所示.

(Ⅱ)该校这次考试的平均成绩为:65×0.04+75×0.12+85×0.16+95×0.3+105×0.2+115×0.06+125×0.08+135×0.04=97,
(Ⅲ)第六组有学生3人,分别记作A1,A2,A3,第八组有学生2人,分别记作B1,B2;
则从中任取2人的所有基本事件为 (A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(A1,A2),(A1,A3),A2,A3),(B1,B2)共10个.
分差在(10分)以上,表示所选2人来自不同组,其基本事件有6个:(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),
所以从中任意抽取2人,分差在(10分)以上的概率P=
| 6 |
| 10 |
| 3 |
| 5 |
点评:本题主要考查了频率分布直方图、平均数、古典概型的概率问题,属于基础题.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
有7个座位连成一排,4人就坐,要求恰有两个空位相邻且甲乙两人不坐在相邻座位,则不同的坐法种数是( )
| A、512 | B、480 |
| C、408 | D、336 |
已知全集为R,集合A={-1,0,1},B={x|(
)x≤1},则A∩∁RB等于( )
| 1 |
| 2 |
| A、(-∞,0) |
| B、[0,+∞) |
| C、{-1} |
| D、{0,1} |
过点P(4,2)作圆x2+y2=4的两条切线,切点分别为A、B,O为坐标原点,则△PAB的外接圆方程是( )
| A、(x-2)2+(y-1)2=5 |
| B、(x-4)2+(y-2)2=20 |
| C、(x+2)2+(y+1)2=5 |
| D、(x+4)2+(y+2)2=20 |