题目内容
设a是实数,函数f(x)=ax2+(a+1)x-2lnx.
(1)当a=1时,求函数f(x)的单调区间;
(2)当a=2时,过原点O作曲线y=f(x)的切线,求切点的横坐标;
(3)设定义在D上的函数y=g(x)在点P(x0,y0)处的切线方程为l:y=h(x),当x≠x0时,若
<0在D内恒成立,则称点P为函数y=g(x)的“巧点”.当a=-
时,试问函数y=f(x)是否存在“巧点”?若存在,请求出“巧点”的横坐标;若不存在,说明理由.
(1)当a=1时,求函数f(x)的单调区间;
(2)当a=2时,过原点O作曲线y=f(x)的切线,求切点的横坐标;
(3)设定义在D上的函数y=g(x)在点P(x0,y0)处的切线方程为l:y=h(x),当x≠x0时,若
| g(x)-h(x) |
| x-x0 |
| 1 |
| 4 |
考点:利用导数研究曲线上某点切线方程,利用导数研究函数的单调性
专题:综合题,导数的综合应用
分析:(1)求导数,利用导数的正负,可得函数f(x)的单调区间;
(2)设切点,可得切线的斜率k=4m+3-
,利用直线OM的斜率为
,建立方程,即可求切点的横坐标;
(3)分类讨论,根据“巧点”的定义结合函数的单调性,即可得出结论.
(2)设切点,可得切线的斜率k=4m+3-
| 2 |
| m |
| 2m2+3m-2lnm |
| m |
(3)分类讨论,根据“巧点”的定义结合函数的单调性,即可得出结论.
解答:
解:(1)当a=1时,f′(x)=
(x>0),…(1分)
由f′(x)>0得:x>
;由f′(x)<0得:0<x<
. …(2分)
所以,f(x)的单调增区间为(
,+∞),单调减区间为(0,
). …(3分)
(2)当a=2时,设切点为M (m,n).
f′(x)=4x+3-
( x>0),所以,切线的斜率k=4m+3-
.
又直线OM的斜率为
,…(5分)
所以,4m+3-
=
,即m2+lnm-1=0,
又函数y=m2+lnm-1在(0,+∞)上递增,且m=1是一根,所以是唯一根,
所以,切点横坐标为1. …(7分)
(3)a=-
时,由函数y=f(x)在其图象上一点P(x0,y0)处的切线方程为:
y=(-
x0+
-
)(x-x0)-
x02+
x0-2ln x0. …(8分)
令h(x)=(-
x0+
-
)(x-x0)-
x02+
x0-2ln x0,
设F(x)=f(x)-h(x),则F(x0)=0.
且F′(x)=f′(x)-h′(x)=-
x+
-
-(-
x0+
-
)
=-
(x-x0)-(
-
)=-
(x-x0) (x-
) …(10分)
当0<x0<2时,
>x0,F(x)在(x0,
)上单调递增,从而有F(x)>F(x0)=0,所以,
>0;
当x0>2时,
<x0,F(x)在(
,x0)上单调递增,从而有F(x)<F(x0)=0,所以,
>0.
因此,y=f(x)在(0,2)和(2,+∞)上不存在“巧点”. …(13分)
当x0=2时,F′(x)=-
≤0,所以函数F(x)在(0,+∞)上单调递减.
所以,x>2时,F(x)<F(2)=0,
<0;0<x<2时,F(x)>F(2)=0,
<0.
因此,点(2,f(2))为“巧点”,其横坐标为2. …(16分)
| 2(x2+x-1) |
| x |
由f′(x)>0得:x>
-1+
| ||
| 2 |
-1+
| ||
| 2 |
所以,f(x)的单调增区间为(
-1+
| ||
| 2 |
-1+
| ||
| 2 |
(2)当a=2时,设切点为M (m,n).
f′(x)=4x+3-
| 2 |
| x |
| 2 |
| m |
又直线OM的斜率为
| 2m2+3m-2lnm |
| m |
所以,4m+3-
| 2 |
| m |
| 2m2+3m-2lnm |
| m |
又函数y=m2+lnm-1在(0,+∞)上递增,且m=1是一根,所以是唯一根,
所以,切点横坐标为1. …(7分)
(3)a=-
| 1 |
| 4 |
y=(-
| 1 |
| 2 |
| 3 |
| 4 |
| 2 |
| x0 |
| 1 |
| 4 |
| 3 |
| 4 |
令h(x)=(-
| 1 |
| 2 |
| 3 |
| 4 |
| 2 |
| x0 |
| 1 |
| 4 |
| 3 |
| 4 |
设F(x)=f(x)-h(x),则F(x0)=0.
且F′(x)=f′(x)-h′(x)=-
| 1 |
| 2 |
| 3 |
| 4 |
| 2 |
| x |
| 1 |
| 2 |
| 3 |
| 4 |
| 2 |
| x0 |
=-
| 1 |
| 2 |
| 2 |
| x |
| 2 |
| x0 |
| 1 |
| 2x |
| 4 |
| x0 |
当0<x0<2时,
| 4 |
| x0 |
| 4 |
| x0 |
| F(x) |
| x-x0 |
当x0>2时,
| 4 |
| x0 |
| 4 |
| x0 |
| F(x) |
| x-x0 |
因此,y=f(x)在(0,2)和(2,+∞)上不存在“巧点”. …(13分)
当x0=2时,F′(x)=-
| (x-2)2 |
| 2x |
所以,x>2时,F(x)<F(2)=0,
| F(x) |
| x-2 |
| F(x) |
| x-2 |
因此,点(2,f(2))为“巧点”,其横坐标为2. …(16分)
点评:正确理解导数的几何意义、“巧点”的意义及熟练掌握利用导数研究函数的单调性是解题的关键.

练习册系列答案
相关题目
已知集合A={x|x(3-x)>0},集合B={y|y=2x+2},则A∩B=( )
| A、{x|2<x<3} |
| B、{x|x<0或x>2} |
| C、{x|x>3} |
| D、{x|x<0或x≥2} |
 某校在一次期末数学统测中,为统计学生的考试情况,从学校的2000名学生中随机抽取50名学生的考试成绩,被测学生成绩全部介于60分到140分之间(满分150分),将统计结果按如下方式分成八组:第一组[60,70),第二组[70,80),…,第八组[130,140],如图是按上述分组方法得到的频率分布直方图的一部分.
某校在一次期末数学统测中,为统计学生的考试情况,从学校的2000名学生中随机抽取50名学生的考试成绩,被测学生成绩全部介于60分到140分之间(满分150分),将统计结果按如下方式分成八组:第一组[60,70),第二组[70,80),…,第八组[130,140],如图是按上述分组方法得到的频率分布直方图的一部分.  如图,PA为⊙O的切线,A为切点,PBC是过点O的割线,PA=10,PB=5.求:
如图,PA为⊙O的切线,A为切点,PBC是过点O的割线,PA=10,PB=5.求:
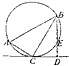 如图,在△ABC中,∠C=90°,∠A=60°,AB=10,过C作△ABC的外接圆的切线CD,BD⊥CD,BD与外接圆交于点E,则线段BE的长为
如图,在△ABC中,∠C=90°,∠A=60°,AB=10,过C作△ABC的外接圆的切线CD,BD⊥CD,BD与外接圆交于点E,则线段BE的长为