题目内容
有三种卡片分别写有数字1,10和100.设m为正整数,从上述三种卡片中选取若干张,使得这些卡片上的数字之和为m.考虑不同的选法种数,例如当m=11时,有如下两种选法:“一张卡片写有1,另一张卡片写有10”或“11张写有1的卡片”,则选法种数为2.
(1)若m=100,直接写出选法种数;
(2)设n为正整数,记所选卡片的数字和为100n的选法种数为an.当n≥2时,求数列{an}的通项公式.
(1)若m=100,直接写出选法种数;
(2)设n为正整数,记所选卡片的数字和为100n的选法种数为an.当n≥2时,求数列{an}的通项公式.
考点:数列的应用,数列递推式
专题:综合题,等差数列与等比数列
分析:(1)分类讨论,只取数字1或10或100时;取1和10,由此可得结论;
(2)考虑当数字和为200时,选法种数,可得数字总和为100n对应的选法种数为an,数字总和为100(n+1)对应的选法种数为an+1,满足an=10n+1+an-1,从而可得数列通项,
(2)考虑当数字和为200时,选法种数,可得数字总和为100n对应的选法种数为an,数字总和为100(n+1)对应的选法种数为an+1,满足an=10n+1+an-1,从而可得数列通项,
解答:
解:(1)分类讨论,只取数字1或10或100时,共3种;取1和10,可分为1个10,2个10,…9个10,共9种
∴相应的选法种数为3+9=12种; …(3分)
(2)若至少选一张写有100的卡片时,则除去1张写有100的卡片,其余数字之和为100(n-1),
有an-1种选法;若不选含有100的卡片,则有10n+1种选法.
所以,an=10n+1+an-1,…(8分)
从而,an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1
=10n+1+10(n-1)+1+…+10×2+1+a1
=10
+n-1+a1
=5n2+6n+1
所以,{an}的通项公式是an=5n2+6n+1. …(10分)
∴相应的选法种数为3+9=12种; …(3分)
(2)若至少选一张写有100的卡片时,则除去1张写有100的卡片,其余数字之和为100(n-1),
有an-1种选法;若不选含有100的卡片,则有10n+1种选法.
所以,an=10n+1+an-1,…(8分)
从而,an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1
=10n+1+10(n-1)+1+…+10×2+1+a1
=10
| (n+2)(n-1) |
| 2 |
=5n2+6n+1
所以,{an}的通项公式是an=5n2+6n+1. …(10分)
点评:本题考查数列的应用,考查分类讨论的数学思想,正确分类是关键.

练习册系列答案
相关题目
 某校在一次期末数学统测中,为统计学生的考试情况,从学校的2000名学生中随机抽取50名学生的考试成绩,被测学生成绩全部介于60分到140分之间(满分150分),将统计结果按如下方式分成八组:第一组[60,70),第二组[70,80),…,第八组[130,140],如图是按上述分组方法得到的频率分布直方图的一部分.
某校在一次期末数学统测中,为统计学生的考试情况,从学校的2000名学生中随机抽取50名学生的考试成绩,被测学生成绩全部介于60分到140分之间(满分150分),将统计结果按如下方式分成八组:第一组[60,70),第二组[70,80),…,第八组[130,140],如图是按上述分组方法得到的频率分布直方图的一部分. 
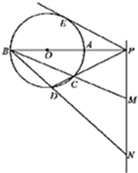 如图,已知PE是⊙O的切线,切点为E,PAB,PCD都是⊙O的割线,且PAB经过圆心O,过点P直线与直线BC,BD分别交于点M,N,且PE2=PM•PN.
如图,已知PE是⊙O的切线,切点为E,PAB,PCD都是⊙O的割线,且PAB经过圆心O,过点P直线与直线BC,BD分别交于点M,N,且PE2=PM•PN.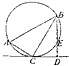 如图,在△ABC中,∠C=90°,∠A=60°,AB=10,过C作△ABC的外接圆的切线CD,BD⊥CD,BD与外接圆交于点E,则线段BE的长为
如图,在△ABC中,∠C=90°,∠A=60°,AB=10,过C作△ABC的外接圆的切线CD,BD⊥CD,BD与外接圆交于点E,则线段BE的长为