题目内容
10.已知tanα=7,求值.(1)$\frac{sinα+cosα}{2sinα-cosα}$=$\frac{8}{13}$;
(2)sin2α+sinαcosα+3cos2α=$\frac{59}{50}$.
分析 (1)利用同角三角函数基本关系式,化简为正切函数的形式,代入求解即可.
(2)利用平方关系式,化为正切函数的形式,代入求解即可.
解答 解:(1)∵tanα=7,
∴$\frac{sinα+cosα}{2sinα-cosα}$=$\frac{tanα+1}{2tanα-1}$=$\frac{7+1}{14-1}$=$\frac{8}{13}$.
(2)sin2α+sinαcosα+3cos2α=$\frac{si{n}^{2}α+sinαcosα+3co{s}^{2}α}{si{n}^{2}α+co{s}^{2}α}$=$\frac{ta{n}^{2}α+tanα+3}{ta{n}^{2}α+1}$=$\frac{49+7+3}{49+1}$=$\frac{59}{50}$.
故答案为:$\frac{8}{13}$;$\frac{59}{50}$.
点评 本题考查同角三角函数基本关系式的应用,三角函数化简求值,考查计算能力.

练习册系列答案
相关题目
20.经过1小时,时针旋转的角是( )
| A. | 第一象限角 | B. | 第二象限角 | C. | 第三象限角 | D. | 第四象限角 |
18.命题“?x∈R,cosx<$\frac{1}{2}$”的否定是( )
| A. | ?x<R,cosx≥$\frac{1}{2}$ | B. | ?x∈R,cosx>$\frac{1}{2}$ | C. | ?x<R,cosx≥$\frac{1}{2}$ | D. | ?x∈R,cosx>$\frac{1}{2}$ |
2.执行如图的程序后,输出的值是( )


| A. | 17 | B. | 19 | C. | 21 | D. | 23 |
19.过点P(2,1)且在x,y轴上的截距相等的直线方程为( )
| A. | x-2y=0 | B. | 2x-y=0或x+y-3=0 | C. | x+y-3=0 | D. | x-2y=0或x+y-3=0 |
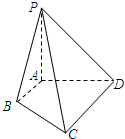 如图,已知PA⊥平面ABCD,PA=AB=AD=$\frac{1}{2}$CD=1,∠BAD=∠ADC=90°.
如图,已知PA⊥平面ABCD,PA=AB=AD=$\frac{1}{2}$CD=1,∠BAD=∠ADC=90°.