题目内容
6.已知函数f(x)=$\sqrt{2}$sin(ωx-$\frac{π}{4}$)(ω>0)最小正周期是π,(1)求ω的值.
(2)若x∈[0,$\frac{π}{2}$]且f(x)=0,求x的值.
分析 (1)根据f(x)解析式,利用周期公式,即可求得ω的值;
(2)由(1)求得函数解析式,令f(x)=0,求得x=$\frac{kπ}{2}$+$\frac{π}{8}$,k∈Z,根据x的取值范围,即可求得x的值.
解答 解:(1)f(x)=$\sqrt{2}$sin(ωx-$\frac{π}{4}$),
由周期公式T=$\frac{2π}{ω}$,即ω=$\frac{2π}{T}$=2,
∴ω=2;
∴f(x)=$\sqrt{2}$sin(2x-$\frac{π}{4}$),
(2)f(x)=0,即sin(2x-$\frac{π}{4}$)=0,
∴2x-$\frac{π}{4}$=kπ,k∈Z,
∴x=$\frac{kπ}{2}$+$\frac{π}{8}$,k∈Z,
∵x∈[0,$\frac{π}{2}$],
∴$x=\frac{π}{8}$.
点评 本题考查正弦函数周期公式,求正弦函数的函数值,考查计算能力,属于基础题.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
14.已知函数f(x)=|ln(x-1)|,若实数a,b(a<b)满足f(a)=f(b),则-a+5b的取值范围为( )
| A. | (5,8) | B. | (8,9) | C. | (5,9) | D. | (8,+∞) |
18.命题“?x∈R,cosx<$\frac{1}{2}$”的否定是( )
| A. | ?x<R,cosx≥$\frac{1}{2}$ | B. | ?x∈R,cosx>$\frac{1}{2}$ | C. | ?x<R,cosx≥$\frac{1}{2}$ | D. | ?x∈R,cosx>$\frac{1}{2}$ |
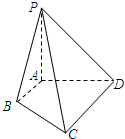 如图,已知PA⊥平面ABCD,PA=AB=AD=$\frac{1}{2}$CD=1,∠BAD=∠ADC=90°.
如图,已知PA⊥平面ABCD,PA=AB=AD=$\frac{1}{2}$CD=1,∠BAD=∠ADC=90°.