题目内容
设a，b，c均为正数，且a+b+c=1，证明
+
+
≥
．
| a2 |
| a+b |
| b2 |
| b+c |
| c2 |
| c+a |
| 1 |
| 2 |
考点：不等式的证明
专题：证明题,不等式的解法及应用
分析：a+b+c=1，所以
+
+
=
（
+
+
）（a+b+b+c+c+a），利用基本不等式，即可证明结论．
| a2 |
| a+b |
| b2 |
| b+c |
| c2 |
| c+a |
| 1 |
| 2 |
| a2 |
| a+b |
| b2 |
| b+c |
| c2 |
| c+a |
解答：
证明：∵a+b+c=1，
∴
+
+
=
（
+
+
）（a+b+b+c+c+a）
=
[a2+b2+c2+
+
+
+
+
+
]
≥
（a2+b2+c2+2ab+2bc+2ac）=
（a+b+c）2=
．
当且仅当a=b=c时，等号成立．
∴
| a2 |
| a+b |
| b2 |
| b+c |
| c2 |
| c+a |
| 1 |
| 2 |
| a2 |
| a+b |
| b2 |
| b+c |
| c2 |
| c+a |
=
| 1 |
| 2 |
| a2(b+c) |
| a+b |
| a2(c+a) |
| a+b |
| b2(a+b) |
| b+c |
| b2(c+a) |
| b+c |
| c2(a+b) |
| c+a |
| c2(b+c) |
| c+a |
≥
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
当且仅当a=b=c时，等号成立．
点评：本题考查不等式的证明，考查基本不等式的运用，掌握基本不等式的使用条件是关键．
练习册系列答案
培优三好生系列答案
相关题目
数列{an}为等差数列，a1，a2，a3为等比数列，a5=1，则a10=（ ）
| A、5 | B、-1 | C、0 | D、1 |
如果函数f（x+1）是偶函数，那么函数y=f（2x）的图象的一条对称轴是直线（ ）
| A、x=-1． | ||
| B、x=1 | ||
C、x=-
| ||
D、x=
|
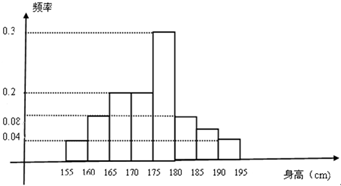现从某校高三年年级学生中随机抽取n名同学测量身高，据测量，所有学生的身高均介于155至195cm之间，将测量结果按如下方式分成8组；第一组；[155，160）；第二组[160，165）；…，第八组[190，195]．如图是按上述分组得到的条形图，其中第五组有15名同学．